Page 12 - Focus SPM 2022 - Additional Mathematics

Additional Mathematics SPM Chapter 1 Functions
(d) y = 2x + 1
y = (x – 1) + 2 is a continuous function. There is no
2
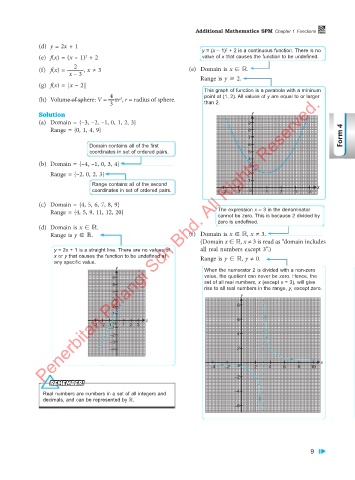
(e) f(x) = (x – 1) + 2 value of x that causes the function to be undefined.
2
2
(f) f(x) = , x ≠ 3 (e) Domain is x  R.
x – 3
Range is y > 2.
(g) f(x) = | x – 2 |
This graph of function is a parabola with a mininum
4
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
(h) Volume of sphere: V = πr , r = radius of sphere. point at (1, 2). All values of y are equal to or larger
3
3 than 2.
Solution y
(a) Domain = {–3, –2, –1, 0, 1, 2, 3} 9
Range = {0, 1, 4, 9} 8
7 Form 4
Domain contains all of the first 6
coordinates in set of ordered pairs. 5
4
(b) Domain = {–4, –1, 0, 3, 4} 3
Range = {–2, 0, 2, 3} 2
1
Range contains all of the second
coordinates in set of ordered pairs. –2 –1 0 1 2 3 4 x

(c) Domain = {4, 5, 6, 7, 8, 9}
Range = {4, 5, 9, 11, 12, 20} The expression x – 3 in the denominator
cannot be zero. This is because 2 divided by
zero is undefined.
(d) Domain is x  R.
Range is y  R. (f) Domain is x  R, x ≠ 3.
(Domain x  R, x ≠ 3 is read as “domain includes
y = 2x + 1 is a straight line. There are no values of all real numbers except 3”.)
x or y that causes the function to be undefined at Range is y  R, y ≠ 0.
any specific value.
y When the numerator 2 is divided with a non-zero

6 value, the quotient can never be zero. Hence, the
5 set of all real numbers, x (except x = 3), will give
rise to all real numbers in the range, y, except zero.
4
y
3
2 8
1
x 6
–3 –2 –1 0 1 2 3
–1
–2 4
–3
–4 2

x
–4 –2 0 2 4 6 8 10
–2
REMEMBER!
Real numbers are numbers in a set of all integers and –4
decimals, and can be represented by R.
–6

9