Page 65 - 3 MATH (Ganesh M. Chaure)

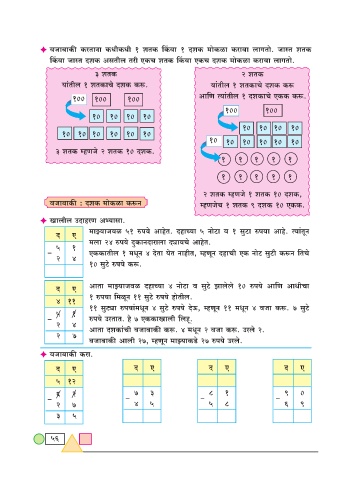
F dOm~mH$s H$aVmZm H$YrH$Yr 1 eVH$ qH$dm 1 XeH$ ‘moH$im H$amdm bmJVmo. OmñV eVH$
qH$dm OmñV XeH$ AgVrb Var EH$M eVH$ qH$dm EH$M XeH$ ‘moH$im H$amdm bmJVmo.

3 eVH 2 eVH$

¶m§Vrb 1 eVH$mMo XeH$ H$ê$. ¶m§Vrb 1 eVH$mMo XeH$ H$ê$

100 100 100 Am{U ˶m§Vrb 1 XeH$mMo EH$H$ H$ê$.
100
100
10 10 10 10
10 10 10 10
10 10 10 10 10 10
10 10 10 10 10 10
3 eVH$ åhUOo 2 eVH$ 10 XeH$.
1 1 1 1 1

1 1 1 1 1

2 eVH$ åhUOo 1 eVH$ 10 XeH$,
dOm~mH$s : XeH$ ‘moH$im H$ê$Z åhUOoM 1 eVH$ 9 XeH$ 10 EH$H$.

F Imbrb CXmhaU Aä¶mgm.

‘m¶mOdi 51 én¶o AmhoV. XhmÀ¶m 5 ZmoQ>m d 1 gwQ>m én¶m Amho. ˶m§VyZ
X E
‘bm 24 én¶o XþH$mZXmambm Xçm¶Mo AmhoV.
5 1
- EH$H$mVrb 1 ‘YyZ 4 XoVm ¶oV ZmhrV, åhUyZ XhmMr EH$ ZmoQ> gwQ>r H$ê$Z {VMo
2 4
10 gwQ>o én¶o H$ê$.

X E AmVm ‘m¶mOdi XhmÀ¶m 4 ZmoQ>m d gwQ>o Pmbobo 10 én¶o Am{U AmYrMm
1 én¶m {‘iyZ 11 gwQ>o én¶o hmoVrb.
4 11
11 gwQ>çm én`m§_YyZ 4 gwQ>o én`o XoD$, åhUyZ 11 ‘YyZ 4 dOm H$ê$. 7 gwQ>o
5 1
- én`o CaVmV. ho 7 EH$H$mImbr {bhÿ.
2 4 AmVm XeH$m§Mr dOm~mH$s H$ê$. 4 ‘YyZ 2 dOm H$ê$. Cabo 2.

2 7
dOm~mH$s Ambr 27, åhUyZ _mÂ`mH$S>o 27 én`o Cabo.

F dOm~mH$s H$am.

X E X E X E X E

5 12
6 2 7 3 8 1 9 0
- - - -
2 7 4 5 5 8 6 9
3 5

56