Page 14 - 1202 Question Bank Additional Mathematics Form 5

Section B
[30 marks]
Answer any three questions from this section.

——–——.
8. (a) (i) Find lim 3 + 2x – x 2 [1 mark]
x → 3 x – 3
dy
(ii) Given that x = t + t and y = 2t + 1, where t . 0, find —– in terms of y and hence, find the approximate
2
dx
change in y if x decreases from 2 to 1.98 when t = 1. [3 marks]
2
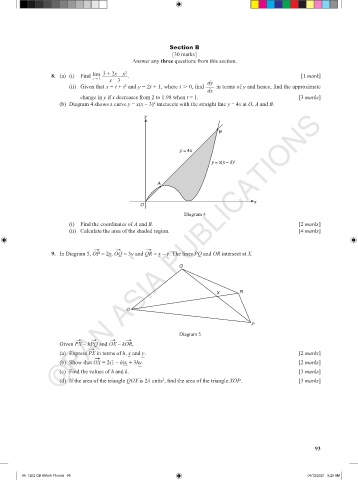
(b) Diagram 4 shows a curve y = x(x – 3) intersects with the straight line y = 4x at O, A and B.
©PAN ASIA PUBLICATIONS
y
B

y = 4x

y = x(x – 3) 2

A

x
O
Diagram 4
(i) Find the coordinates of A and B. [2 marks]
(ii) Calculate the area of the shaded region. [4 marks]

→ → →
9. In Diagram 5, OP = 2x, OQ = 3y and QR = x – y. The lines PQ and OR intersect at X.
~
~
~
~
Q

X R

O

P
Diagram 5
→ → → →
Given PX = hPQ and OX = kOR,
→
(a) Express PX in terms of h, x and y. [2 marks]
~
→ ~
(b) Show that OX = 2(1 – h)x + 3hy. [2 marks]
~
~
(c) Find the values of h and k. [3 marks]
2
(d) If the area of the triangle QOX is 24 units , find the area of the triangle XOP. [3 marks]

93

09_1202 QB AMath F5.indd 93 04/12/2021 9:25 AM