Page 382 - Math Smart - 7

Let us use coordinate points to describe rotations of 2D shapes.
Example 4

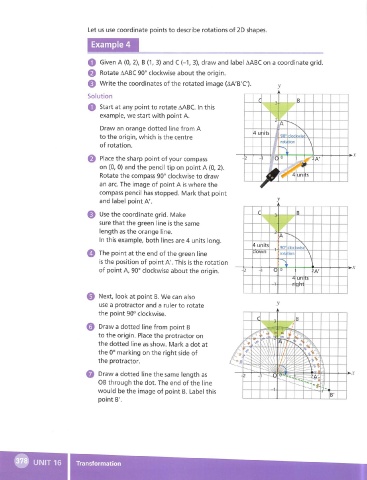
Q Given A (0, 2), B (1, 3) and C (-1, 3), draw and label AABCon a coordinate grid.
Q Rotate AABC 90° clockwise about the origin.
Q Write the coordinates of the rotated image (AA'B'C).

Solution
O Start at any point to rotate AABC. In this
example, we start with point A.

Draw an orange dotted line from A
to the origin, which is the centre
of rotation.
*-x
Q Place the sharp point of your compass
on {0, 0) and the pencil tip on point A (0, 2).
Rotate the compass 90° clockwise to draw
an arc. The image of point A is where the
compass pencil has stopped. Mark that point
and label point A'.

Q Use the coordinate grid. Make r R
sure that the green line is the same % -*• ^ y"
length as the orange line.
A
In this example, both lines are 4 units long. N.
s
4 u lits
90° cloc ;wis€ N
Q The point at the end of the green line Jo\ t/ii rot2tion \
is the position of point A'. This is the rotation N
of point A, 90° clockwise about the origin. 2 *1 0 0 A'
A un ts

Next, look at point B. We can also
use a protractor and a ruler to rotate
the point 90° clockwise.
C B
@ Draw a dotted line from point B immr nmmr r
to the origin. Place the protractor on TS «0 ^ h
'
t N 100
the dotted line as show. Mark a dot at ;\\ \J • S"? \
///
the 0° marking on the right side of '// ^ r / N •?<'
the protractor. :\i !// S''.
Draw a dotted line the same length as 2
-
OB through the dot. The end of the line
"s-
would be the image of point B. Label this
B'
point B'.

UNIT 16 Transformation