Page 35 - RPT TINGKATAN 1

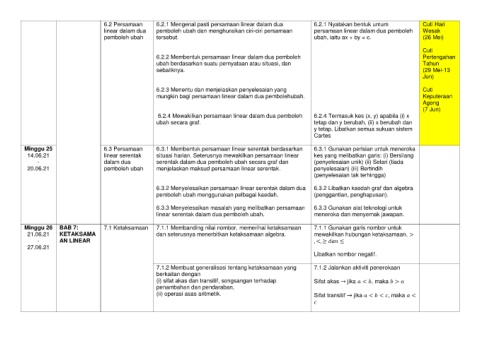
6.2 Persamaan 6.2.1 Mengenal pasti persamaan linear dalam dua 6.2.1 Nyatakan bentuk umum Cuti Hari
linear dalam dua pemboleh ubah dan menghuraikan ciri-ciri persamaan persamaan linear dalam dua pemboleh Wesak
pemboleh ubah tersebut. ubah, iaitu ax + by = c. (26 Mei)

Cuti
6.2.2 Membentuk persamaan linear dalam dua pemboleh Pertengahan
ubah berdasarkan suatu pernyataan atau situasi, dan Tahun
sebaliknya. (29 Mei-13
Jun)

6.2.3 Menentu dan menjelaskan penyelesaian yang Cuti
mungkin bagi persamaan linear dalam dua pembolehubah. Keputeraan
Agong
(7 Jun)
6.2.4 Mewakilkan persamaan linear dalam dua pemboleh 6.2.4 Termasuk kes (x, y) apabila (i) x
ubah secara graf. tetap dan y berubah, (ii) x berubah dan
y tetap. Libatkan semua sukuan sistem
Cartes

Minggu 25 6.3 Persamaan 6.3.1 Membentuk persamaan linear serentak berdasarkan 6.3.1 Gunakan perisian untuk meneroka
14.06.21 linear serentak situasi harian. Seterusnya mewakilkan persamaan linear kes yang melibatkan garis: (i) Bersilang
- dalam dua serentak dalam dua pemboleh ubah secara graf dan (penyelesaian unik) (ii) Selari (tiada
20.06.21 pemboleh ubah menjelaskan maksud persamaan linear serentak. penyelesaian) (iii) Bertindih
(penyelesaian tak terhingga)

6.3.2 Menyelesaikan persamaan linear serentak dalam dua 6.3.2 Libatkan kaedah graf dan algebra
pemboleh ubah menggunakan pelbagai kaedah. (penggantian, penghapusan).

6.3.3 Menyelesaikan masalah yang melibatkan persamaan 6.3.3 Gunakan alat teknologi untuk
linear serentak dalam dua pemboleh ubah. meneroka dan menyemak jawapan.

Minggu 26 BAB 7: 7.1 Ketaksamaan 7.1.1 Membanding nilai nombor, memerihal ketaksamaan 7.1.1 Gunakan garis nombor untuk
21.06.21 KETAKSAMA dan seterusnya menerbitkan ketaksamaan algebra. mewakilkan hubungan ketaksamaan, >
- AN LINEAR , <, ≥ ≤
27.06.21
Libatkan nombor negatif.

7.1.2 Membuat generalisasi tentang ketaksamaan yang 7.1.2 Jalankan aktiviti penerokaan
berkaitan dengan
(i) sifat akas dan transitif, songsangan terhadap Sifat akas → jika < , maka >
penambahan dan pendaraban,
(ii) operasi asas aritmetik. Sifat transitif → jika < < , maka <