Page 41 - ACE YR IGCSE A TOP APPR' TO ADD MATH

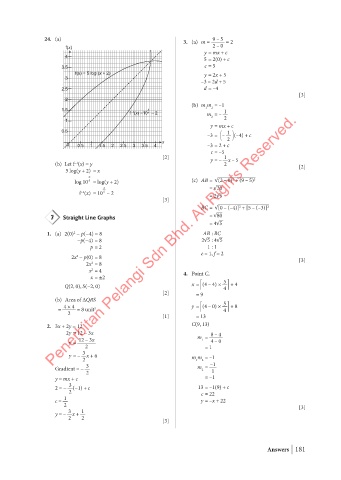
24. (a) 3. (a) m = 9 – 5 = 2
f(x) 2 – 0
y = mx + c
4 5 = 2(0) + c

3.5 c = 5
f(x) = 5 log (x + 2) y = 2x + 5
3
–3 = 2d + 5
2.5 d = –4
[3]
2
(b) m m = –1
1.5 x 1 2 1
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
f (x) =10 – 2 m = –
5
–1
1 2 2
y = mx + c
0.5 1
2
1
–3 = – (–4) + c
2
0 0.5 1 1.5 2 2.5 3 3.5 4 x –3 = 2 + c
c = –5
1
[2] y = – x – 5
(b) Let f (x) = y 2 [2]
−1
5 log(y + 2) = x
x 2 2
log 10 = log(y + 2) (c) AB = √(2 – 0) + (9 – 5)
5
x = √20
5
f (x) = 10 − 2 = 2√5
−1
[3]
BC = √[0 – (–4)] + [5 – (–3)]
2
2
7 Straight Line Graphs = √80
= 4√5
2
1. (a) 2(0) − p(−4) = 8 AB : BC
−p(−4) = 8 2√5 : 4√5
p = 2 1 : 1
e = 1, f = 2
2
2x − p(0) = 8 [3]
2
2x = 8
2
x = 4 4. Point C,
x = ±2
3
Q(2, 0), S(−2, 0) x = (4 – 4) × 5 4 + 4
4
[2] = 9
(b) Area of ΔQRS 5
3
= 4 × 4 = 8 unit y = (4 – 0) × 4 4 + 8
2
2 [1] = 13
2. 3x + 2y = 12 C(9, 13)
2y = 12 − 3x m = 8 – 4
y = 12 – 3x 1 4 – 0
2 = 1
3
y = – x + 6
2 m m = –1
2
1
Gradient = − 3 m = –1
2
2 1
y = mx + c = –1
3
2 = − (−1) + c 13 = –1(9) + c
2 c = 22
1
c = y = –x + 22
2 [3]
3
y = – x + 1
2 2 [3]
Answers 181

Answers Add Math.indd 181 14/03/2022 12:29 PM