Page 78 - 3 MATH (Ganesh M. Chaure)
P. 78
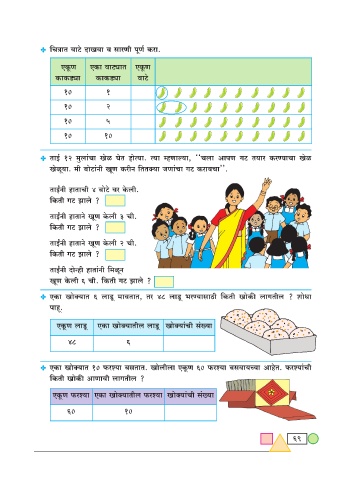
D {MÌmV dmQ>o XmIdm d gmaUr nyU© H$am.
$EHy$U EH$m dmQ>çmV EHy$U
H$mH$S>çm H$mH$S>çm dmQ>o
10 1
10 2
10 5
10 10
D VmB© 12 _wbm§Mm Ioi KoV hmoË`m. Ë`m åhUmë`m, ""Mbm AmnU JQ> V¶ma H$aʶmMm Ioi
Ioiy¶m. ‘r ~moQ>m§Zr IyU H$arZ {VV³¶m OUm§Mm JQ> H$am`Mm''.
VmBªZr hmVmMr 4 ~moQ>o da Ho$br.
{H$Vr JQ> Pmbo ?
VmBª©Zr hmVmZo IyU Ho$br 3 Mr.
{H$Vr JQ> Pmbo ?
VmBª©Zr hmVmZo IyU Ho$br 2 Mr.
{H$Vr JQ> Pmbo ?
VmBª©Zr XmoÝhr hmVm§Zr {‘iyZ
IyU Ho$br 6 Mr. {H$Vr JQ> Pmbo ?
D EH$m Imo³¶mV 6 bmSy> ‘mdVmV, Va 48 bmSy> ^aÊ`mgmR>r {H$Vr ImoH$s bmJVrb ? emoYm
nmhÿ.
EHy$U bmSy> EH$m Imo³¶mVrb bmSy> ImoŠ`m§Mr g§»`m
48 6 >
D EH$m Imo³¶mV 10 ’$aí¶m ~gVmV. Imobrbm EHy$U 60 ’$aí¶m ~gdm¶À¶m AmhoV. ’$aí¶m§Mr
{H$Vr ImoH$s AmUmdr bmJVrb ?
EHy$U ’$aí¶m EH$m Imo³¶mVrb ’$aí¶m ImoŠ`m§Mr g§»`m
60 10 >
69