Page 93 - Euclid's Elements of Geometry

ST EW gþ.

ELEMENTS BOOK 3

αἱ ΓΒ, ΔΒ. ACD have been drawn through (the segments), and let
CB and DB have been joined.

∆ D
Γ C

Α Β A B
kdþ
᾿Επεὶ οὖν ὅμοιόν ἐστι τὸ ΑΓΒ τμῆμα τῷ ΑΔΒ τμήματι, Therefore, since segment ACB is similar to segment
ὅμοια δὲ τμήματα κύκλων ἐστὶ τὰ δεχόμενα γωνίας ἴσας, ADB, and similar segments of circles are those accept-
ἴση ἄρα ἐστὶν ἡ ὑπὸ ΑΓΒ γωνία τῇ ὑπὸ ΑΔΒ ἡ ἐκτὸς τῇ ing equal angles [Def. 3.11], angle ACB is thus equal
ἐντός· ὅπερ ἐστὶν ἀδύνατον. to ADB, the external to the internal. The very thing is
Οὐκ ἄρα ἐπὶ τῆς αὐτῆς εὐθείας δύο τμήματα κύκλων impossible [Prop. 1.16].
ὅμοια καὶ ἄνισα συσταθήσεται ἐπὶ τὰ αὐτὰ μέρη· ὅπερ ἔδει Thus, two similar and unequal segments of circles
δεῖξαι. cannot be constructed on the same side of the same
straight-line.

Proposition 24
.
Τὰ ἐπὶ ἴσων εὐθειῶν ὅμοια τμήματα κύλων ἴσα ἀλλήλοις Similar segments of circles on equal straight-lines are
ἐστίν. equal to one another.
Ε E

Α Β A B

Η G
Ζ F

Γ ∆ C D
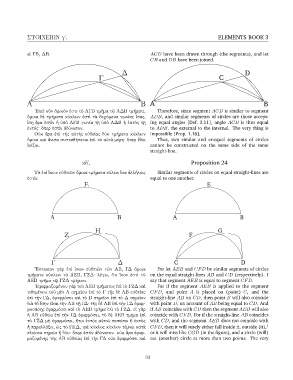
῎Εστωσαν γὰρ ἐπὶ ἴσων εὐθειῶν τῶν ΑΒ, ΓΔ ὅμοια For let AEB and CFD be similar segments of circles
τμήματα κύκλων τὰ ΑΕΒ, ΓΖΔ· λέγω, ὅτι ἴσον ἐστὶ τὸ on the equal straight-lines AB and CD (respectively). I
ΑΕΒ τμῆμα τῷ ΓΖΔ τμήματι. say that segment AEB is equal to segment CFD.
᾿Εφαρμοζομένου γὰρ τοῦ ΑΕΒ τμήματος ἐπὶ τὸ ΓΖΔ καὶ For if the segment AEB is applied to the segment
τιθεμένου τοῦ μὲν Α σημείου ἐπὶ τὸ Γ τῆς δὲ ΑΒ εὐθείας CFD, and point A is placed on (point) C, and the
ἐπὶ τὴν ΓΔ, ἐφαρμόσει καὶ τὸ Β σημεῖον ἐπὶ τὸ Δ σημεῖον straight-line AB on CD, then point B will also coincide
διὰ τὸ ἴσην εἶναι τὴν ΑΒ τῇ ΓΔ· τῆς δὲ ΑΒ ἐπὶ τὴν ΓΔ ἐφαρ- with point D, on account of AB being equal to CD. And
μοσάσης ἐφαρμόσει καὶ τὸ ΑΕΒ τμῆμα ἐπὶ τὸ ΓΖΔ. εἰ γὰρ if AB coincides with CD then the segment AEB will also
ἡ ΑΒ εὐθεῖα ἐπὶ τὴν ΓΔ ἐφαρμόσει, τὸ δὲ ΑΕΒ τμῆμα ἐπὶ coincide with CFD. For if the straight-line AB coincides
τὸ ΓΖΔ μὴ ἐφαρμόσει, ἤτοι ἐντὸς αὐτοῦ πεσεῖται ἢ ἐκτὸς with CD, and the segment AEB does not coincide with
ἢ παραλλάξει, ὡς τὸ ΓΗΔ, καὶ κύκλος κύκλον τέμνει κατὰ CFD, then it will surely either fall inside it, outside (it), †
πλείονα σημεῖα ἢ δύο· ὅπερ ἐστίν ἀδύνατον. οὐκ ἄρα ἐφαρ- or it will miss like CGD (in the figure), and a circle (will)
μοζομένης τῆς ΑΒ εὐθείας ἐπὶ τὴν ΓΔ οὐκ ἐφαρμόσει καὶ cut (another) circle at more than two points. The very

93