Page 96 - text book form physics kssm 2020

For a body in circular motion, a force acts on the body in a direction towards the centre of
the circle. Th is force is called centripetal force.
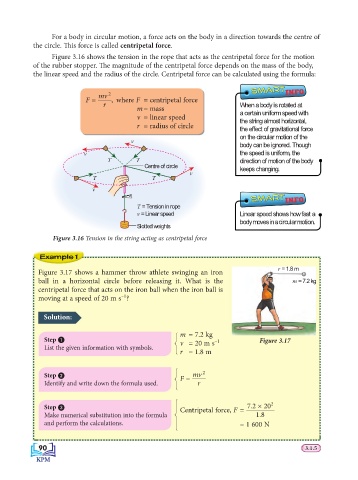
Figure 3.16 shows the tension in the rope that acts as the centripetal force for the motion
of the rubber stopper. Th e magnitude of the centripetal force depends on the mass of the body,
the linear speed and the radius of the circle. Centripetal force can be calculated using the formula:
SMART INFO
SMART
mv 2
F = , where F = centripetal force
r When a body is rotated at
m = mass a certain uniform speed with
v = linear speed the string almost horizontal,
r = radius of circle the effect of gravitational force
on the circular motion of the
v
body can be ignored. Though
v the speed is uniform, the
T T direction of motion of the body
Centre of circle keeps changing.
v
T T
v
SMART INFO
SMART
T = Tension in rope
v = Linear speed Linear speed shows how fast a
body moves in a circular motion.
Slotted weights

Figure 3.16 Tension in the string acting as centripetal force

Example 1
r = 1.8 m
Figure 3.17 shows a hammer throw athlete swinging an iron
ball in a horizontal circle before releasing it. What is the m = 7.2 kg
centripetal force that acts on the iron ball when the iron ball is
–1
moving at a speed of 20 m s ?
Solution:

m = 7.2 kg
Step 123 r = 1.8 m –1 Figure 3.17
v = 20 m s
List the given information with symbols.

Step F = mv 2
Identify and write down the formula used. 123 r

Step Centripetal force, F = 7.2 × 20 2
Make numerical substitution into the formula 14243 1.8
and perform the calculations. = 1 600 N

90
90
90 3.1.5
90
3.1.5