Page 21 - 1202 Bank Soalan Matematik Tambahan Tingkatan 5

Apabila h = 1, = ——— 3. (a) BD = x sin α
3
20 3x 9 DE = DB sin α
—– – —– = 1 1 – — = (x sin α)(sin α)
x
5
4
100 – 3x = 5x 12 = x sin α
2
2
3x + 5x – 100 = 0 = – —– (b) EF = DE sin α
2
5
(3x + 20)(x – 5) = 0 p = x sin α
3
x = 5 15. P(rosak) = —–, n = 5 ∴ x sin α, x sin α, x sin α
10
2
3
x sin α
2
1
dV
54(5)
2
1
2
—– = 120 – —–––– ————–– (a) P(X = 0) = 0.1681 r = ———– = sin α
p
x sin α
20
dh 5 1 – —– – —2 5 C —– 0 q 5 x sin α
3
0 1 10 2 1 10 2
—– = 0.1681
3
5
5
2
r = ———– = sin α
q
5
x sin α
1
7 2
= –150 – — —– = 0.7 (c) T = HG 2
10
5
5
1 ©PAN ASIA PUBLICATIONS
= 107.14 Maka, p = 3 q = 7 = x sin α
a
dh
dV
1 2
—– = 107.14 —– (b) 7 biji mentol baik, 3 biji mentol (d) S = ——–
1 – r
∞
dt dt x sin α
dV
Diberi —– = 21 cm s rosak = ————
3 –1
1 – sin α
dt Jika 3 biji mentol yang rosak
dh
1 2
21 = 107.14 —– disusun bersama, bilangan cara Jika x = 8, α = 60°
8 sin 60°
dt
S = ————–
8!
dh
—– = 0.196 cm s –1 = —– = 8 ∞ 1 – sin 60°
7!
dt (c) p + q + 0.2 + 2p + q = 1 8AB 3
——
2
14. (a) BC = 10 sin θ 3p + 2q = 0.8 ........... S = ———–
AB = 10 kos θ P(X < 2) = p + q = 0.55 – 0.2 .....2 ∞ 1 – —–
AB 3
(i) Luas, L 2p + 2q = 0.7 ................3 2
1
= —(10) sin θ (10 kos θ)  – 3: p = 0.1 8AB 3(2 + AB 3)
2 q = 0.35 – 0.1 = 0.25 S = ———————
∞
= 50 sin θ kos θ (2 – AB 3)(2 + AB 3)
= (25 sin 2θ) cm 2 S = 24 + 16AB 3
∞
25AB 3 Kertas 2 x – 2
(ii) 25 sin 2θ = ——– 4. (a) y = ab
2 Bahagian A log y = log a + (x – 2) log b
10
10
10
AB 3 Y = log y, X = x – 2, m = log b,
sin 2θ = —– 1. x y z 10 10
2 x + y + z = 16 ................................. c = log a
10
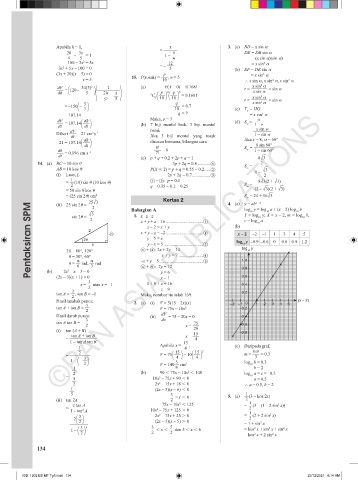
z – 2 = x + y (b)
2
3 x + y – z = –2 .................................2 x – 2 –2 –1 1 3 4 5
2θ y – 5 = x log y –0.9 –0.6 0 0.6 0.9 1.2
1 y – x = 5 ...................................3 10
2θ = 60°, 120°  + 2: 2x + 2y = 14 log y
10
θ = 30°, 60° x + y = 7 ......................4
π
π
θ = — rad, — rad –x + y = 5 .......................................5 1.0
6 3 4 + 5: 2y = 12 0.8
(b) 2x – x – 3 = 0 y = 6
2
(2x – 3)(x + 1) = 0 x = 1 0.6
3
x = — atau x = –1 1 + 6 + z = 16 0.4
2
z = 9
3
tan A = —, tan B = –1 Maka, nombor itu ialah 169. 0.2
2
Hasil tambah punca: 2. (a) (i) V = 5(15 – 2x)(x) (x – 2)
1
tan A + tan B = — V = 75x – 10x 2 –2 –1 0 1 2 3 4 5
–0.2
2
dV
Hasil darab punca: (ii) —– = 75 – 20x = 0 –0.4
dx
3
tan A tan B = – — 75
2 x = —– –0.6
(i) tan (A + B) 20 –0.8
15
tan A + tan B x = —–
= —————— 4
1 – tan A tan B Apabila x = —–, (c) Daripada graf,
15
1
— 15 4 15 2 0.9
1 4 2
2
1 4 2
= ————– V = 75 —– – 10 —– m = —– = 0.3
3
3
1
2 2
1 – – — V = 140— cm 3 log b = 0.3
5
10
8
1
— (b) 90 , 75x – 10x , 140 b = 2
2
2
= —— 10x – 75x + 90 , 0 log a = c = –0.3
10
2
5
— a = 0.5
2 2x – 15x + 18 , 0 ∴ a = 0.5, b = 2
2
= — (2x – 3)(x – 6) , 0 1
5
3
2
2
(ii) tan 2A — < x , 6 5. (a) —(3 – kos 2x)
1
2
2 tan A 75x – 10x , 125 = —(3 – (1 – 2 sin x))
2
= ———— 2 2
1 – tan A 10x – 75x + 125 . 0 1 2
2
2
3
1 2 2
2
2 — 2x – 15x + 25 . 0 = —(2 + 2 sin x)
(2x – 5)(x – 5) . 0
2
= ———— 2 3 5 = 1 + sin x
3
1 2 2
2
2
2
1 – — — , x , — dan 5 , x , 6 = kos x + sin x + sin x
2
2
2
2
= kos x + 2 sin x
134
10B_1202 BS MT Tg5.indd 134 23/12/2021 8:14 AM