Page 268 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

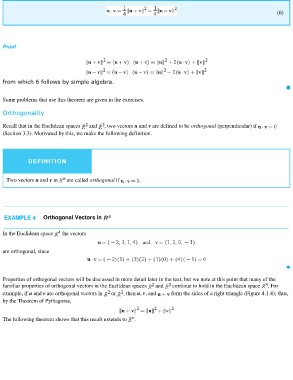
(6)

Proof

from which 6 follows by simple algebra.

Some problems that use this theorem are given in the exercises.

Orthogonality

Recall that in the Euclidean spaces and , two vectors u and v are defined to be orthogonal (perpendicular) if
(Section 3.3). Motivated by this, we make the following definition.

DEFINITION .
Two vectors u and v in are called orthogonal if

EXAMPLE 4 Orthogonal Vectors in
In the Euclidean space the vectors
are orthogonal, since

Properties of orthogonal vectors will be discussed in more detail later in the text, but we note at this point that many of the
familiar properties of orthogonal vectors in the Euclidean spaces and continue to hold in the Euclidean space . For

example, if u and v are orthogonal vectors in or , then u, v, and form the sides of a right triangle (Figure 4.1.4); thus,

by the Theorem of Pythagoras,

The following theorem shows that this result extends to .