Page 279 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

4.2 In this section we shall begin the study of functions of the form ,

LINEAR where the independent variable x is a vector in and the dependent variable
TRANSFORMATIONS
FROM Rn TO Rm w is a vector in . We shall concentrate on a special class of such functions

called “linear transformations.” Linear transformations are fundamental in the

study of linear algebra and have many important applications in physics,

engineering, social sciences, and various branches of mathematics.

Functions from to R

Recall that a function is a rule f that associates with each element in a set A one and only one element in a set B. If f associates

the element b with the element a, then we write and say that b is the image of a under f or that is the value of f at

a. The set A is called the domain of f and the set B is called the codomain of f. The subset of B consisting of all possible values

for f as a varies over A is called the range of f. For the most common functions, A and B are sets of real numbers, in which case f

is called a real-valued function of a real variable. Other common functions occur when B is a set of real numbers and A is a set
of vectors in , , or, more generally, . Some examples are shown in Table 1. Two functions and are regarded as

equal, written , if they have the same domain and for all a in the domain.

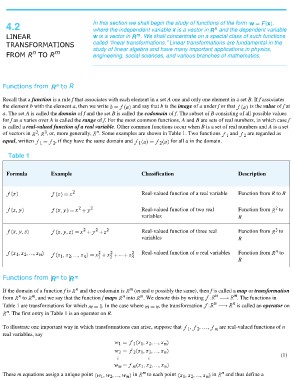
Table 1

Formula Example Classification Description

Real-valued function of a real variable Function from R to R

Real-valued function of two real Function from to
variables R

Real-valued function of three real Function from to
variables R

Real-valued function of n real variables Function from to
R

Functions from to

If the domain of a function f is and the codomain is (m and n possibly the same), then f is called a map or transformation

from to , and we say that the function f maps into . We denote this by writing . The functions in

Table 1 are transformations for which . In the case where , the transformation is called an operator on

. The first entry in Table 1 is an operator on R.

To illustrate one important way in which transformations can arise, suppose that , , …, are real-valued functions of n
real variables, say

(1)

These m equations assign a unique point in to each point in and thus define a