Page 285 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

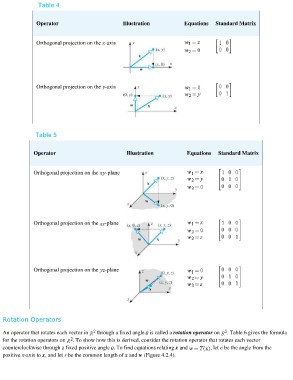
Table 4 Illustration Equations Standard Matrix

Operator

Orthogonal projection on the x-axis

Orthogonal projection on the y-axis

Table 5 Illustration Equations Standard Matrix

Operator

Orthogonal projection on the -plane

Orthogonal projection on the -plane
Orthogonal projection on the -plane

Rotation Operators

An operator that rotates each vector in through a fixed angle is called a rotation operator on . Table 6 gives the formula

for the rotation operators on . To show how this is derived, consider the rotation operator that rotates each vector

counterclockwise through a fixed positive angle . To find equations relating x and , let be the angle from the

positive x-axis to x, and let r be the common length of x and w (Figure 4.2.4).