Page 313 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

Observe that if A is the standard matrix for T, then 7 can be written as
from which it follows that

The eigenvalues of T are precisely the eigenvalues of its standard matrix A.

x is an eigenvector of T corresponding to if and only if x is an eigenvector of A corresponding to .

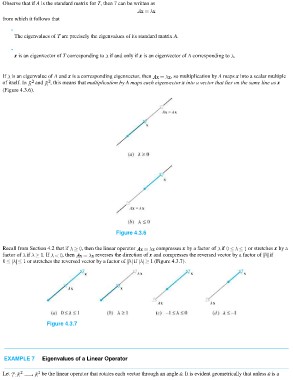
If is an eigenvalue of A and x is a corresponding eigenvector, then , so multiplication by A maps x into a scalar multiple

of itself. In and , this means that multiplication by A maps each eigenvector x into a vector that lies on the same line as x

(Figure 4.3.6).

Figure 4.3.6

Recall from Section 4.2 that if , then the linear operator compresses x by a factor of if or stretches x by a

factor of if . If , then reverses the direction of x and compresses the reversed vector by a factor of if

or stretches the reversed vector by a factor of if (Figure 4.3.7).

Figure 4.3.7

EXAMPLE 7 Eigenvalues of a Linear Operator
Let be the linear operator that rotates each vector through an angle . It is evident geometrically that unless is a