Page 360 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition
P. 360
Proof (b) Each vector is a linear combination of since we can write
Therefore, the subspace W contains each of the vectors . Let be any other subspace
that contains . Since is closed under addition and scalar multiplication, it must contain
all linear combinations of . Thus, contains each vector of W.
We make the following definition.
DEFINITION
If is a set of vectors in a vector space V, then the subspace W of V consisting of all linear
combinations of the vectors in S is called the space spanned by , and we say that the vectors
span W. To indicate that W is the space spanned by the vectors in the set , we write
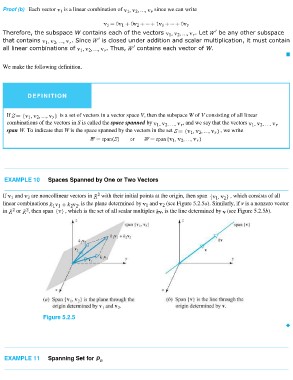
EXAMPLE 10 Spaces Spanned by One or Two Vectors
If and are noncollinear vectors in with their initial points at the origin, then span , which consists of all
linear combinations , is the plane determined by and (see Figure 5.2.5a). Similarly, if v is a nonzero vector
in or , then span , which is the set of all scalar multiples , is the line determined by (see Figure 5.2.5b).
Figure 5.2.5
EXAMPLE 11 Spanning Set for