Page 175 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
Š‡ ƒ”‡ƒ ‘ˆ –Š‡ •‡ –‘” ‘ˆ –Š‡ ‹” Ž‡ •Š‘™ ‹ ȏ ‹‰ ͳǤ͹͸Ȑ ‹• †‡”‹˜‡† ƒ• ˆ‘ŽŽ‘™•ǣ

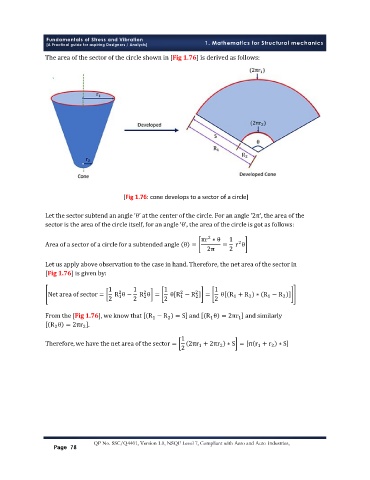
[Fig 1.76: cone develops to a sector of a circle]

Let the sector subtend an angle ‘θ’ at the center of the circle. For an angle ‘2π’, the area of the
sector is the area of the circle itself, for an angle ‘θ’, the area of the circle is got as follows:
2
πr ∗ θ 1
2
Area of a sector of a circle for a subtended angle θ = = r θ
2π 2
Let us apply above observation to the case in hand. Therefore, the net area of the sector in
[Fig 1.76] is given by:

1 1 1 1
2
2
2
2
Net area of sector = R θ − R θ = θ R − R = θ R + R ∗ R − R
1
2
1
2
2 1 2 2 2 1 2 2

From the [Fig 1.76], we know that R − R = S and R θ = 2πr and similarly
1
1
2
1
R θ = 2πr .
2
2
1
Therefore, we have the net area of the sector = 2πr + 2πr ∗ S = π r + r ∗ S
2 1 2 1 2

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 78