Page 31 - Physics Form 5 KSSM_Neat

Solving Problems Involving Forces in Equilibrium CHAPTER 1

LET’S ANSWER
Example 1 LET’S ANSWER
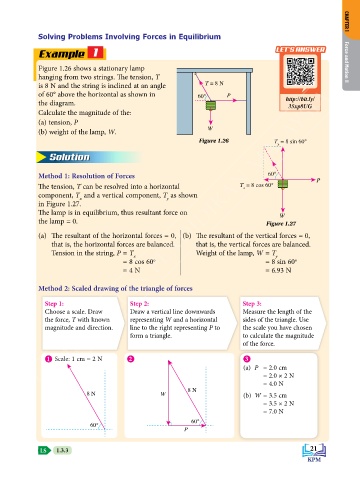
Figure 1.26 shows a stationary lamp Force and Motion II
hanging from two strings. The tension, T
is 8 N and the string is inclined at an angle T = 8 N
KEMENTERIAN PENDIDIKAN MALAYSIA
of 60° above the horizontal as shown in 60° P
the diagram. http://bit.ly/
35xp8UG
Calculate the magnitude of the:
(a) tension, P
(b) weight of the lamp, W. W
Figure 1.26 T = 8 sin 60°
y
Solution

Method 1: Resolution of Forces 60°
P
The tension, T can be resolved into a horizontal T = 8 cos 60°
x
component, T and a vertical component, T as shown
x
y
in Figure 1.27.
The lamp is in equilibrium, thus resultant force on
W
the lamp = 0. Figure 1.27
(a) The resultant of the horizontal forces = 0, (b) The resultant of the vertical forces = 0,
that is, the horizontal forces are balanced. that is, the vertical forces are balanced.
Tension in the string, P = T x Weight of the lamp, W = T y
= 8 cos 60 o = 8 sin 60 o
= 4 N = 6.93 N

Method 2: Scaled drawing of the triangle of forces

Step 1: Step 2: Step 3:
Choose a scale. Draw Draw a vertical line downwards Measure the length of the
the force, T with known representing W and a horizontal sides of the triangle. Use
magnitude and direction. line to the right representing P to the scale you have chosen
form a triangle. to calculate the magnitude
of the force.
1 Scale: 1 cm = 2 N 2 3
Skala: 1 cm = 4 N
(a) P = 2.0 cm
= 2.0 × 2 N
= 4.0 N
8 N
8 N W (b) W = 3.5 cm
= 3.5 × 2 N
= 7.0 N
60°
60°
P

LS 1.3.3 21