Page 4 - Top Class Mathematics F4

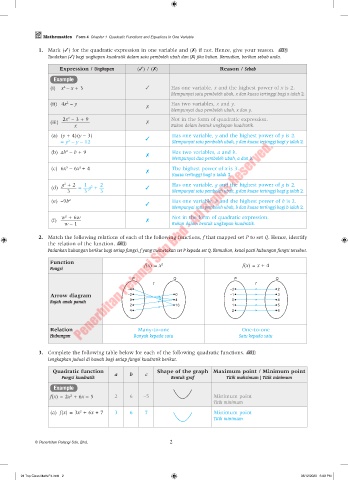
Mathematics Form 4 Chapter 1 Quadratic Functions and Equations in One Variable

1. Mark (✓) for the quadratic expression in one variable and (✗) if not. Hence, give your reason. PL 1
Tandakan (✓) bagi ungkapan kuadratik dalam satu pemboleh ubah dan (✗) jika bukan. Kemudian, berikan sebab anda.
Expression / Ungkapan (✓) / (✗) Reason / Sebab

Example
(i) x – x + 3 ✓ Has one variable, x and the highest power of x is 2.
2
Mempunyai satu pemboleh ubah, x dan kuasa tertinggi bagi x ialah 2.
(ii) 4x – y Has two variables, x and y.
2
✗
Mempunyai dua pemboleh ubah, x dan y.
2
2x – 3 + 9 Not in the form of quadratic expression.
(iii) ✗
x Bukan dalam bentuk ungkapan kuadratik.
(a) (y + 4)(y – 3) ✓ Has one variable, y and the highest power of y is 2.
= y – y – 12 Mempunyai satu pemboleh ubah, y dan kuasa tertinggi bagi y ialah 2.
2
(b) ab – b + 9 Has two variables, a and b.
2
✗
Mempunyai dua pemboleh ubah, a dan b.
(c) 6x – 6x + 4 The highest power of x is 3.
2
3
✗
Kuasa tertinggi bagi x ialah 3.
2
g + 2 1 2 Has one variable, g and the highest power of g is 2.
(d) = g + ✓
2
3 3 3 Mempunyai satu pemboleh ubah, g dan kuasa tertinggi bagi g ialah 2.
(e) –9b 2 Has one variable, b and the highest power of b is 2.
✓
Mempunyai satu pemboleh ubah, b dan kuasa tertinggi bagi b ialah 2.
2
w + 6w Not in the form of quadratic expression.
(f) ✗
w – 1 Bukan dalam bentuk ungkapan kuadratik.
2. Match the following relations of each of the following functions, f that mapped set P to set Q. Hence, identify
the relation of the function. PL 1
Padankan hubungan berikut bagi setiap fungsi, f yang memetakan set P kepada set Q. Kemudian, kenal pasti hubungan fungsi tersebut.

Function f(x) = x 2 f(x) = x + 4
Fungsi

P Q P Q
f f
–4 –2 2
Arrow diagram –2 0 –1 3
Rajah anak panah 0 4 0 4
2 16 1 5
4 2 6

Relation Many-to-one One-to-one
Hubungan Banyak kepada satu Satu kepada satu

3. Complete the following table below for each of the following quadratic functions. PL 1
Lengkapkan jadual di bawah bagi setiap fungsi kuadratik berikut.
Quadratic function a b c Shape of the graph Maximum point / Minimum point
Fungsi kuadratik Bentuk graf Titik maksimum / Titik minimum
Example
f(x) = 2x + 6x – 5 2 6 –5 Minimum point
2
Titik minimum
2
(a) f(x) = 3x + 6x + 7 3 6 7 Minimum point
Titik minimum

© Penerbitan Pelangi Sdn. Bhd. 2

01 Top Class Math F4.indd 2 05/12/2020 5:00 PM