Page 64 - ACE YR IGCSE A TOP APPR' TO ADD MATH

19. (a) dV = 50 y
dt
dV
2
= 0.3h + 1.3 7
dh
When h = 8, 6
dV = dV × dh
dt dh dt 5
dh = 50
dt 0.3(8) + 1.3 4
2
= 2.44 cm s
–1
[3] 3
= 1 (b) 50 = (0.3h + 1.3) × 0.2
2
2
0.3h + 1.3 = 250 2
2
= √3
h = 250 – 1.3
2
= √(7) – 0.3 1
2
h = 28.8 cm
2
2
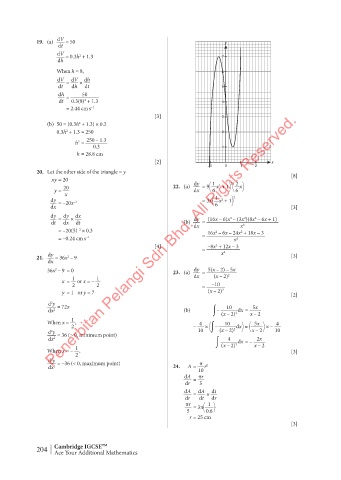
= 1 8 + 3 [2] –1 0 1 2 x
2
1 20. Let the other side of the triangle = y [8]
= 2 2 xy = 20 dy 1 2 2
x
2
= y = 20 22. (a) dx = 9 1 6 x + 1 2 1 2
6
2 x
(b) dy = 3x 1 1 x + 1
2
2
2
–2
1 = –20x 6
dx [3]
==
dy = dy × dx dy (16x – 6)x – (3x )(8x – 6x + 1)
2
2
3
dt dx dt (b) dx = x 6
= –20(5) × 0.3 16x – 6x – 24x + 18x – 3
–2
2
2
=
2 Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
= –0.24 cm s
–1
x
4
[4] = –8x + 12x – 3
2
21. dy = 36x – 9 x 4 [3]
2
dx
36x – 9 = 0 23. (a) dy = 5(x – 2) – 5x
2
1 1 dx (x – 2) 2
x = or x = –
2 2 = –10
y = 1 or y = 7 (x – 2) 2 [2]
d y = 72x
2
10
5x
dx 2 (b) – (x – 2) 2 dx = x – 2
1
When x = , 4 10 5x 4
1
dx =
2 – × – 2 2 1 2 × –
d y 10 (x – 2) x – 2 10
2
dx 2 = 36 (> 0, minimum point) 4 dx = – 2x
1
When x = – , (x – 2) 2 x – 2 [3]
2
d y = –36 (< 0, maximum point) π
2
2
dx 24. A = r
10
dA = πr
dr 5
dA = dA × dt
dr dt dr
πr 1
= 3π 1 2
5 0.6
r = 25 cm
[3]
Cambridge IGCSE
TM
204 Ace Your Additional Mathematics
Answers Add Math.indd 204 14/03/2022 12:29 PM