Page 31 - The Effect of Hydrogen and Hydrides - ebook first test

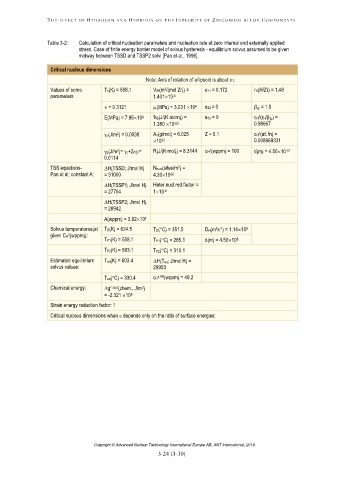
Table 3-2: Calculation of critical nucleation parameters and nucleation rate at zero internal and externally applied
stress. Case of finite energy barrier model of solvus hysteresis - equilibrium solvus assumed to be given
midway between TSSD and TSSP2 solvi [Pan et al., 1996].

Critical nucleus dimensions
Note: Axis of rotation of ellipsoid is about x1:
3
Values of some Tn(K) = 558.1 VZr(m /(mol Zr)) = e11 = 0.172 rH(H/Zr) = 1.48
parameters 1.40110
-5
4
 = 0.3121 (MPa) = 3.031 10 e22 = 0 β = 1.5
δ
E(MPa) = 7.9510 ‘kB(J/(K atom)) = e33 = 0 cH (rH/β ) =
δ
4
δ
-23
1.380 10 0.98667
o
c(J/m ) = 0.0038 Ao(g/mol) = 6.025 Z = 0.1 cH (at. fn) =
2
10 0.008969331
23
2
p(J/m )= c+2i= R(J/(K∙mol)) = 8.3144 cH (wppm) = 100 d(m) = 4.5010
-10
o
0.0114
TSS equations- H(TSSD; J/mol H) Nnucl(sites/m ) =
3
Pan et al; constant A: = 31000 4.3010
22
H(TSSP1; J/mol H) Heter.nucl.red.factor =
= 27704 110
-6
H(TSSP2; J/mol H)
= 28942
A(wppm) = 3.9210
4
Solvus temperatures(at TD(K) = 624.5 TD(C) = 351.5 DH(m s ) = 1.1410
8
2 -1
given CH (wppm)):
0
TP1(K) = 558.1 TP1(C) = 285.1 d(m) = 4.5010
8
TP2(K) = 583.1 TP2(C) = 310.1
Estimated equilibrium Teq(K) = 603.4 H(Teq; J/mol H) =
solvus values: 29953
Teq(C) = 330.4 cH s, eq (wppm) = 49.2
Chemical energy: g , nucl (chem., J/m )
3
= -2.321 10
8
Strain energy reduction factor: 1
Critical nucleus dimensions when  depends only on the ratio of surface energies:

Copyright © Advanced Nuclear Technology International Europe AB, ANT International, 2019.