Page 534 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

510 INTERPOLACIÓN

f (x)
f 3 (x)
2

f (x) = ln x

Valor
1 real

Estimación
cúbica

0
0 5 x

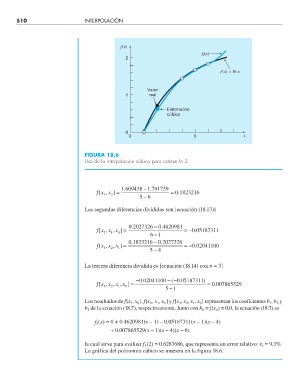
FIGURA 18.6
Uso de la interpolación cúbica para estimar ln 2.

ƒ[,xx ] = . 1 609438 − . 1 791759 = . 0 1823216
3 2 −
56
Las segundas diferencias divididas son [ecuación (18.13)]

ƒ[, ,xx x 0 ] = . 0 2027326 − . 0 4620981 =− . 0 05187311
−
1
2
61
ƒ[,xx 2 , ]x 1 = . 0 1823216 − . 0 2027326 =− . 0 02041100
−
3
54
La tercera diferencia dividida es [ecuación (18.14) con n = 3]
ƒ[,xx , ,x x ] = − . 0 02041100 − −( 0 .05187311 ) = . 0 007865529
3 2 1 0 −
51
Los resultados de f[x , x ], f[x , x , x ] y f[x , x , x , x ] representan los coeficientes b , b y
2
1
3
1
0
0
1
2
0
2
1
b de la ecuación (18.7), respectivamente. Junto con b = f(x ) = 0.0, la ecuación (18.7) es
3
0
0
f (x) = 0 + 0.4620981(x – 1) – 0.05187311(x – 1)(x – 4)
3
+ 0.007865529(x – 1)(x – 4)(x – 6)
la cual sirve para evaluar f (2) = 0.6287686, que representa un error relativo: e t = 9.3%.
3
La gráfica del polinomio cúbico se muestra en la figura 18.6.
6/12/06 13:57:49
Chapra-18.indd 510 6/12/06 13:57:49
Chapra-18.indd 510