Page 82 - Euclid's Elements of Geometry

ST EW gþ.

at point A. ELEMENTS BOOK 3
Θ H

Α ∆ A D
Η G

Β F B
Ζ

Ε E
ibþ

Γ C
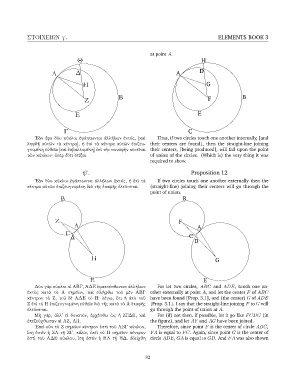
᾿Εὰν ἄρα δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐντός, [καὶ Thus, if two circles touch one another internally, [and
ληφθῇ αὐτῶν τὰ κέντρα], ἡ ἐπὶ τὰ κέντρα αὐτῶν ἐπιζευ- their centers are found], then the straight-line joining
γνυμένη εὐθεῖα [καὶ ἐκβαλλομένη] ἐπὶ τὴν συναφὴν πεσεῖται their centers, [being produced], will fall upon the point
τῶν κύκλων· ὅπερ ἔδει δεῖξαι. of union of the circles. (Which is) the very thing it was
required to show.

Proposition 12
.
᾿Εὰν δύο κύκλοι ἐφάπτωνται ἀλλήλων ἐκτός, ἡ ἐπὶ τὰ If two circles touch one another externally then the
κέντρα αὐτῶν ἐπιζευγνυμένη διὰ τῆς ἐπαφῆς ἐλεύσεται. (straight-line) joining their centers will go through the
point of union.
Β B

Ζ F
Α A
Γ
∆ C
D

Η G

Ε E
Δύο γὰρ κύκλοι οἱ ΑΒΓ, ΑΔΕ ἐφαπτέσθωσαν ἀλλήλων For let two circles, ABC and ADE, touch one an-
ἐκτὸς κατὰ τὸ Α σημεῖον, καὶ εἰλήφθω τοῦ μὲν ΑΒΓ other externally at point A, and let the center F of ABC
κέντρον τὸ Ζ, τοῦ δὲ ΑΔΕ τὸ Η· λέγω, ὅτι ἡ ἀπὸ τοῦ have been found [Prop. 3.1], and (the center) G of ADE
Ζ ἐπὶ τὸ Η ἐπιζευγνυμένη εὐθεῖα διὰ τῆς κατὰ τὸ Α ἐπαφῆς [Prop. 3.1]. I say that the straight-line joining F to G will
ἐλεύσεται. go through the point of union at A.
Μὴ γάρ, ἀλλ᾿ εἰ δυνατόν, ἐρχέσθω ὡς ἡ ΖΓΔΗ, καὶ For (if) not then, if possible, let it go like FCDG (in
ἐπεζεύχθωσαν αἱ ΑΖ, ΑΗ. the figure), and let AF and AG have been joined.
᾿Επεὶ οὖν τὸ Ζ σημεῖον κέντρον ἐστὶ τοῦ ΑΒΓ κύκλου, Therefore, since point F is the center of circle ABC,
ἴση ἐστὶν ἡ ΖΑ τῇ ΖΓ. πάλιν, ἐπεὶ τὸ Η σημεῖον κέντρον FA is equal to FC. Again, since point G is the center of
ἐστὶ τοῦ ΑΔΕ κύκλου, ἴση ἐστὶν ἡ ΗΑ τῇ ΗΔ. ἐδείχθη circle ADE, GA is equal to GD. And FA was also shown

82