Page 269 - Jolliffe I. Principal Component Analysis

10. Outlier Detection, Influential Observations and Robust Estimation
236

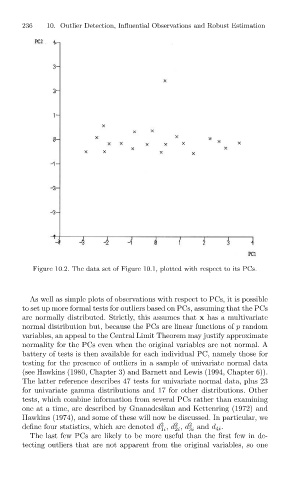
Figure 10.2. The data set of Figure 10.1, plotted with respect to its PCs.

As well as simple plots of observations with respect to PCs, it is possible
to set up more formal tests for outliers based on PCs, assuming that the PCs
are normally distributed. Strictly, this assumes that x has a multivariate
normal distribution but, because the PCs are linear functions of p random
variables, an appeal to the Central Limit Theorem may justify approximate
normality for the PCs even when the original variables are not normal. A
battery of tests is then available for each individual PC, namely those for
testing for the presence of outliers in a sample of univariate normal data
(see Hawkins (1980, Chapter 3) and Barnett and Lewis (1994, Chapter 6)).
The latter reference describes 47 tests for univariate normal data, plus 23
for univariate gamma distributions and 17 for other distributions. Other
tests, which combine information from several PCs rather than examining
one at a time, are described by Gnanadesikan and Kettenring (1972) and
Hawkins (1974), and some of these will now be discussed. In particular, we
2
2
define four statistics, which are denoted d , d , d 2 and d 4i .
1i 2i 3i
The last few PCs are likely to be more useful than the first few in de-
tecting outliers that are not apparent from the original variables, so one