Page 194 - Matematik Tambahan Tingkatan 5 KSSM

SUDUT REFLEKSI

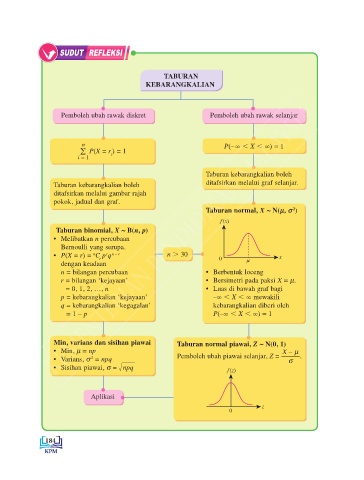
TABURAN
KEBARANGKALIAN

KEMENTERIAN PENDIDIKAN MALAYSIA

Pemboleh ubah rawak diskret Pemboleh ubah rawak selanjar

n P(– ∞ , X , ∞) = 1
∑ P(X = r ) = 1
i = 1 i

Taburan kebarangkalian boleh
Taburan kebarangkalian boleh ditafsirkan melalui graf selanjar.
ditafsirkan melalui gambar rajah
pokok, jadual dan graf.
2
Taburan normal, X ~ N(m, s )

f(x)
Taburan binomial, X ~ B(n, p)
• Melibatkan n percubaan
Bernoulli yang serupa.
r n – r
n
• P(X = r) = C p q n . 30
r 0 x
dengan keadaan μ
n = bilangan percubaan • Berbentuk loceng
r = bilangan ‘kejayaan’ • Bersimetri pada paksi X = m.
= 0, 1, 2, …, n • Luas di bawah graf bagi
p = kebarangkalian ‘kejayaan’ –∞ , X , ∞ mewakili
q = kebarangkalian ‘kegagalan’ kebarangkalian diberi oleh
= 1 – p P(–∞ , X , ∞) = 1

Min, varians dan sisihan piawai Taburan normal piawai, Z ~ N(0, 1)
• Min, m = np X – m
2
• Varians, s = npq Pemboleh ubah piawai selanjar, Z = s .
• Sisihan piawai, s = ! npq

f(z)

Aplikasi
z
0

184