Page 73 - เอกสารประกอบการอบรม คณิตศาสตร์

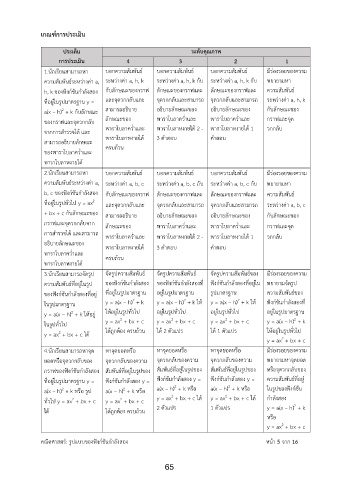
เกณฑ์การประเมิน

ประเด็น ระดับคุณภาพ
การประเมิน 4 3 2 1

1.นักเรียนสามารถหา บอกความสัมพันธ์ บอกความสัมพันธ์ บอกความสัมพันธ์ มีร่องรอยของความ
ความสัมพันธระหว่างค่า a, ระหว่างค่า a, h, k ระหว่างค่า a, h, k กับ ระหว่างค่า a, h, k กับ พยายามหา
์
h, k ของฟังก์ชันก าลังสอง กับลักษณะของกราฟ ลักษณะของกราฟและ ลักษณะของกราฟและ ความสัมพันธ ์
ที่อยู่ในรูปมาตรฐาน y = และจุดวกกลับและ จุดวกกลับและสามารถ จุดวกกลับและสามารถ ระหว่างค่า a, h, k
2
a(x – h) + k กับลักษณะ สามารถอธิบาย อธิบายลักษณะของ อธิบายลักษณะของ กับลักษณะของ
ของกราฟและจุดวกกลับ ลักษณะของ พาราโบลาคว่ าและ พาราโบลาคว่ าและ กราฟและจุด
จากการส ารวจได้ และ พาราโบลาคว่ าและ พาราโบลาหงายได้ 2 - พาราโบลาหงายได้ 1 วกกลับ
สามารถอธิบายลักษณะ พาราโบลาหงายได้ 3 ค าตอบ ค าตอบ
ครบถ้วน
ของพาราโบลาคว่ าและ
พาราโบลาหงายได้

2.นักเรียนสามารถหา บอกความสัมพันธ์ บอกความสัมพันธ์ บอกความสัมพันธ์ มีร่องรอยของความ
์
ความสัมพันธระหว่างค่า a, ระหว่างค่า a, b, c ระหว่างค่า a, b, c กับ ระหว่างค่า a, b, c กับ พยายามหา
b, c ของฟังก์ชันก าลังสอง กับลักษณะของกราฟ ลักษณะของกราฟและ ลักษณะของกราฟและ ความสัมพันธ ์
2
ที่อยู่ในรูปทั่วไป y = ax และจุดวกกลับและ จุดวกกลับและสามารถ จุดวกกลับและสามารถ ระหว่างค่า a, b, c
+ bx + c กับลักษณะของ สามารถอธิบาย อธิบายลักษณะของ อธิบายลักษณะของ กับลักษณะของ
กราฟและจุดวกกลับจาก ลักษณะของ พาราโบลาคว่ าและ พาราโบลาคว่ าและ กราฟและจุด
การส ารวจได้ และสามารถ พาราโบลาคว่ าและ พาราโบลาหงายได้ 2 - พาราโบลาหงายได้ 1 วกกลับ
อธิบายลักษณะของ พาราโบลาหงายได้ 3 ค าตอบ ค าตอบ
พาราโบลาคว่ าและ ครบถ้วน

พาราโบลาหงายได้
์
3.นักเรียนสามารถจัดรูป จัดรูปความสัมพันธ ์ จัดรูปความสัมพันธ ์ จัดรูปความสัมพันธของ มีร่องรอยของความ
ความสัมพันธ์ที่อยู่ในรูป ของฟังก์ชันก าลังสอง ของฟังก์ชันก าลังสองที่ ฟังก์ชันก าลังสองที่อยู่ใน พยายามจัดรูป
์
ของฟังก์ชันก าลังสองที่อยู่ ที่อยู่ในรูปมาตรฐาน อยู่ในรูปมาตรฐาน รูปมาตรฐาน ความสัมพันธของ
2
2
2
ในรูปมาตรฐาน y = a(x – h) + k y = a(x – h) + k ให้ y = a(x – h) + k ให้ ฟังก์ชันก าลังสองที่
2
y = a(x – h) + k ให้อยู่ ให้อยู่ในรูปทั่วไป อยู่ในรูปทั่วไป อยู่ในรูปทั่วไป อยู่ในรูปมาตรฐาน
2
2
2
2
ในรูปทั่วไป y = ax + bx + c y = ax + bx + c y = ax + bx + c y = a(x – h) + k
y = ax + bx + c ได้ ได้ถูกต้อง ครบถ้วน ได้ 2 ตัวแปร ได้ 1 ตัวแปร ให้อยู่ในรูปทั่วไป
2
2
y = ax + bx + c
4.นักเรียนสามารถหาจุด หาจุดยอดหรือ หาจุดยอดหรือ หาจุดยอดหรือ มีร่องรอยของความ
ยอดหรือจุดวกกลับของ จุดวกกลับของความ จุดวกกลับของความ จุดวกกลับของความ พยายามหาจุดยอด
กราฟของฟังก์ชันก าลังสอง สัมพันธ์ที่อยู่ในรูปของ สัมพันธ์ที่อยู่ในรูปของ สัมพันธ์ที่อยู่ในรูปของ หรือจุดวกกลับของ
ที่อยู่ในรูปมาตรฐาน y = ฟังก์ชันก าลังสอง y = ฟังก์ชันก าลังสอง y = ฟังก์ชันก าลังสอง y = ความสัมพันธ์ที่อยู่
2
2
2
2
a(x – h) + k หรือ รูป a(x – h) + k หรือ a(x – h) + k หรือ a(x – h) + k หรือ ในรูปของฟังก์ชัน
2
2
ทั่วไป y = ax + bx + c y = ax + bx + c y = ax + bx + c ได้ y = ax + bx + c ได้ ก าลังสอง 2
2
2
ได้ ได้ถูกต้อง ครบถ้วน 2 ตัวแปร 1 ตัวแปร y = a(x – h) + k
หรือ
2
y = ax + bx + c
คณิตศาสตร์: รูปแบบของฟังก์ชันก าลังสอง หน้า 5 จาก 16

65