Page 18 - Grab Me SPM Add Mathematics Form 4,5

138
©PAN ASIA PUBLICATIONS
Example 11 TIPS

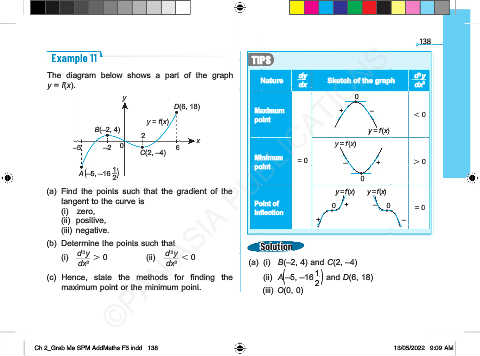
The diagram below shows a part of the graph dy d y
2
y = f(x). Nature dx Sketch of the graph dx 2
y 0
D(6, 18)
Maximum + –  0
y = f(x) point
B(–2, 4) y = f(x)
2 x
–5 –2 0 6 y = f(x)
C(2, –4)
Minimum = 0  0
point – +
1
A(–5, –16 ) –
2 0
(a) Find the points such that the gradient of the y = f(x) y = f(x)
tangent to the curve is Point of + –
(i) zero, inflection 0 0 = 0
(ii) positive, + –
(iii) negative.
(b) Determine the points such that Solution
2
2
(i) d y  0 (ii) d y  0
dx 2 dx 2 (a) (i) B(–2, 4) and C(2, –4)
1
(c) Hence, state the methods for finding the (ii) A(–5, –16 ) and D(6, 18)
maximum point or the minimum point. (iii) O(0, 0) 2

Ch 2_Grab Me SPM AddMaths F5.indd 138 13/05/2022 9:09 AM