Page 12 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
4
Chapter 2 Quadratic Functions Additional Mathematics

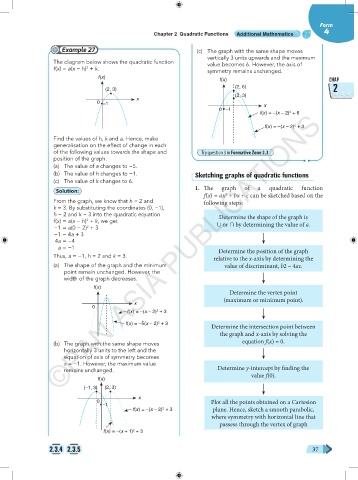
Example 27 (c) The graph with the same shape moves
vertically 3 units upwards and the maximum
The diagram below shows the quadratic function value becomes 6. However, the axis of
f(x) = a(x − h) + k. symmetry remains unchanged.
2
f(x)
f(x) CHAP
(2, 6) 2
(2, 3)
(2, 3)
x
0 –1 x
0 –1
2
f(x) = –(x – 2) + 6
©PAN ASIA PUBLICATIONS
2
f(x) = –(x – 2) + 3
Find the values of h, k and a. Hence, make
generalisation on the effect of change in each
of the following values towards the shape and Try question 3 in Formative Zone 2.3
position of the graph.
(a) The value of a changes to −5.
(b) The value of h changes to −1. Sketching graphs of quadratic functions
(c) The value of k changes to 6.
Solution: 1. The graph of a quadratic function
f(x) = ax + bx + c can be sketched based on the
2
From the graph, we know that h = 2 and following steps:
k = 3. By substituting the coordinates (0, −1),
h = 2 and k = 3 into the quadratic equation Determine the shape of the graph is
f(x) = a(x − h) + k, we get ∪ or ∩ by determining the value of a.
2
−1 = a(0 − 2) + 3
2
−1 = 4a + 3
4a = −4
a = −1 Determine the position of the graph
Thus, a = −1, h = 2 and k = 3. relative to the x-axis by determining the
(a) The shape of the graph and the minimum value of discriminant, b2 – 4ac.
point remain unchanged. However, the
width of the graph decreases.
f(x)
Determine the vertex point
(maximum or minimum point).
x
0
2
f(x) = –(x – 2) + 3
f(x) = –5(x – 2) + 3
2
Determine the intersection point between
the graph and x-axis by solving the
(b) The graph with the same shape moves equation f(x) = 0.
horizontally 3 units to the left and the
equation of axis of symmetry becomes
x = −1. However, the maximum value
remains unchanged. Determine y-intercept by finding the
value f(0).
f(x)
(–1, 3) (2, 3)
x
0 Plot all the points obtained on a Cartesion
–1
f(x) = –(x – 2) + 3 plane. Hence, sketch a smooth parabolic,
2
where symmetry with horizontal line that
. passess through the vertex of graph
2
f(x) = –(x + 1) + 3
2.3.4 2.3.5 37