Page 7 - 1202 Question Bank Mathematics Form 4

PAPER 2

Section A

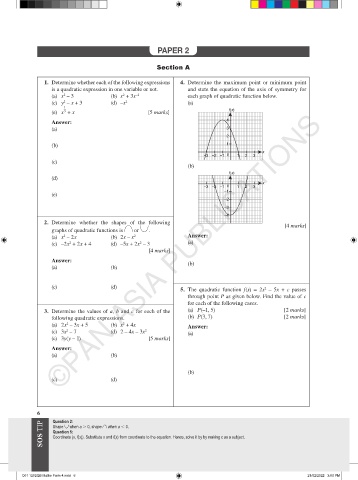
1. Determine whether each of the following expressions 4. Determine the maximum point or minimum point
is a quadratic expression in one variable or not. and state the equation of the axis of symmetry for
2
(a) x – 3 (b) x + 3x –2 each graph of quadratic function below.
2
(c) y – x + 3 (d) –x 2 (a)
2
1
3
(e) x + x [5 marks] f(x)
©PAN ASIA PUBLICATIONS
Answer: 4
(a) 3
2
(b) 1
x
–3 –2 –1 0 1 2 3
(c)
(b)
f(x)
(d)
x
–3 –2 –1 0 1 2 3
–1
(e)
–2
–3
–4
2. Determine whether the shapes of the following
[4 marks]
graphs of quadratic functions is or .
2
(a) x – 2x (b) 2x – x 2 Answer:
2
2
(c) –2x + 2x + 4 (d) –5x + 2x – 3 (a)
[4 marks]
Answer: (b)
(a) (b)

(c) (d) 2
5. The quadratic function f(x) = 2x – 5x + c passes
through point P as given below. Find the value of c
for each of the following cases.
3. Determine the values of a, b and c for each of the (a) P(−1, 5) [2 marks]
following quadratic expressions. (b) P(3, 7) [2 marks]
2
(a) 2x – 3x + 5 (b) x + 4x Answer:
2
(c) 3x – 7 (d) 2 – 4x – 3x 2 (a)
2
(e) 3y(y – 1) [5 marks]
Answer:
(a) (b)

(b)
(c) (d)

6
Question 2:
SOS TIP Question 5:
Shape when a . 0, shape when a , 0.
Coordinate (x, f(x)). Substitute x and f(x) from coordinate to the equation. Hence, solve it by by making c as a subject.

C01 1202QB Maths Form 4.indd 6 21/02/2022 3:00 PM