Page 132 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

Adjoint of a Matrix

In a cofactor expansion we compute by multiplying the entries in a row or column by their cofactors and adding the

resulting products. It turns out that if one multiplies the entries in any row by the corresponding cofactors from a different

row, the sum of these products is always zero. (This result also holds for columns.) Although we omit the general proof, the

next example illustrates the idea of the proof in a special case.

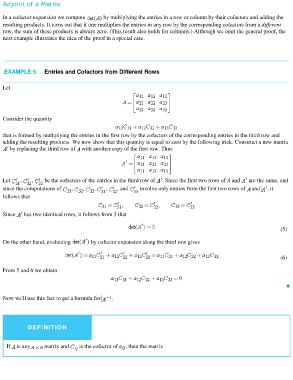
EXAMPLE 5 Entries and Cofactors from Different Rows
Let

Consider the quantity

that is formed by multiplying the entries in the first row by the cofactors of the corresponding entries in the third row and
adding the resulting products. We now show that this quantity is equal to zero by the following trick. Construct a new matrix

by replacing the third row of with another copy of the first row. Thus

Let , , be the cofactors of the entries in the third row of . Since the first two rows of A and are the same, and
since the computations of , , , , , and involve only entries from the first two rows of and , it
follows that

Since has two identical rows, it follows from 3 that

On the other hand, evaluating by cofactor expansion along the third row gives (5)
(6)

From 5 and 6 we obtain

Now we'll use this fact to get a formula for .

DEFINITION
If is any matrix and is the cofactor of , then the matrix