Page 133 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

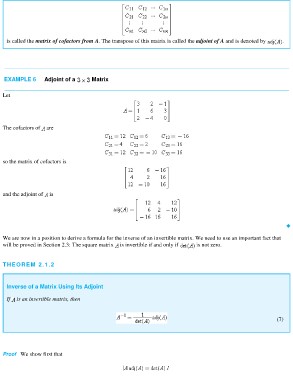
is called the matrix of cofactors from A. The transpose of this matrix is called the adjoint of A and is denoted by .

EXAMPLE 6 Adjoint of a Matrix
Let

The cofactors of are

so the matrix of cofactors is
and the adjoint of is

We are now in a position to derive a formula for the inverse of an invertible matrix. We need to use an important fact that

will be proved in Section 2.3: The square matrix is invertible if and only if is not zero.

THEOREM 2.1.2

Inverse of a Matrix Using Its Adjoint
If is an invertible matrix, then

(7)

Proof We show first that