Page 459 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition
P. 459
Show that matrix 5 generates the weighted Euclidean inner product .
31.
The following is a proof of part (c) of Theorem 6.1.1. Fill in each blank line with the name of an
32. inner product axiom that justifies the step.
Hypothesis: Let u and v be vectors in a real inner product space.
Conclusion: .
Proof:
1. _________
2. _________
3. _________
Prove parts (a), (d ), and (e) of Theorem 6.1.1, justifying each step with the name of a vector space
33. axiom or by referring to previously established results.
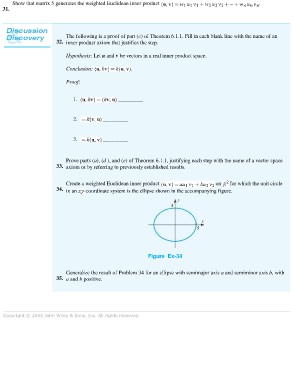
Create a weighted Euclidean inner product on for which the unit circle
34. in an -coordinate system is the ellipse shown in the accompanying figure.
Figure Ex-34
Generalize the result of Problem 34 for an ellipse with semimajor axis a and semiminor axis b, with
35. a and b positive.
Copyright © 2005 John Wiley & Sons, Inc. All rights reserved.