Page 38 - Physics Form 5 KSSM_Neat

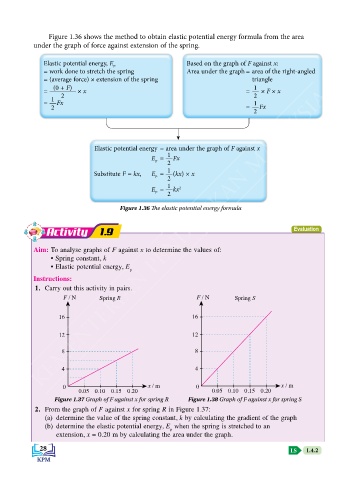
Figure 1.36 shows the method to obtain elastic potential energy formula from the area
under the graph of force against extension of the spring.

Elastic potential energy, E P Based on the graph of F against x:
= work done to stretch the spring Area under the graph = area of the right-angled
= (average force) × extension of the spring triangle
KEMENTERIAN PENDIDIKAN MALAYSIA
= (0 + F) × x = 1 × F × x
1 2 2
= Fx 1
2 = Fx
2

Elastic potential energy = area under the graph of F against x
E = 1 Fx
P 2
Substitute F = kx, E = 1 (kx) × x
2
P
E = 1 kx 2
P 2
Figure 1.36 The elastic potential energy formula

Activity 1.9 Evaluation

Aim: To analyse graphs of F against x to determine the values of:
• Spring constant, k
• Elastic potential energy, E
p
Instructions:
1. Carry out this activity in pairs.
F / N Spring R F / N Spring S

16 16

12 12

8 8

4 4

0 x / m 0 x / m
0.05 0.10 0.15 0.20 0.05 0.10 0.15 0.20
Figure 1.37 Graph of F against x for spring R Figure 1.38 Graph of F against x for spring S
2. From the graph of F against x for spring R in Figure 1.37:
(a) determine the value of the spring constant, k by calculating the gradient of the graph
(b) determine the elastic potential energy, E when the spring is stretched to an
p
extension, x = 0.20 m by calculating the area under the graph.
28 LS 1.4.2