Page 30 - Fisica_1_BGU

Ejemplo 2

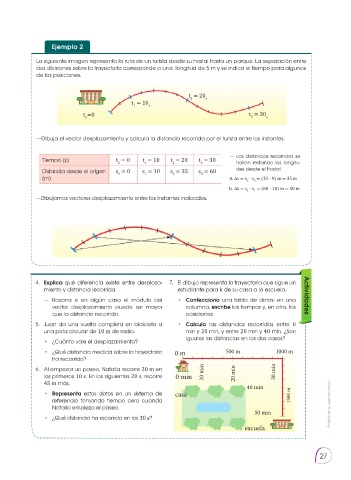
La siguiente imagen representa la ruta de un turista desde su hostal hasta un parque. La separación entre
dos divisiones sobre la trayectoria corresponde a una longitud de 5 m y se indica el tiempo para algunas
de las posiciones.

t = 20
2 s
t = 10
1 s
t =0 t = 30
0 3 s

—Dibuja el vector desplazamiento y calcula la distancia recorrida por el turista entre los instantes:

— Las distancias recorridas se
Tiempo (s) t = 0 t = 10 t = 20 t = 30
0 1 2 3 hallan restando las longitu-
Distancia desde el origen s = 0 s = 10 s = 35 s = 60 des desde el hostal.
(m) 0 1 2 3 a. ∆s = s - s = (35 - 0) m = 35 m
2 0
b. ∆s = s - s = (60 - 10) m = 50 m
3 1
—Dibujamos vectores desplazamiento entre los instantes indicados.

4. Explica qué diferencia existe entre desplaza- 7. El dibujo representa la trayectoria que sigue un
miento y distancia recorrida. estudiante para ir de su casa a la escuela.

— Razona si en algún caso el módulo del • Confecciona una tabla de datos: en una Actividades
vector desplazamiento puede ser mayor columna, escribe los tiempos y, en otra, las
que la distancia recorrida. posiciones.

5. Juan da una vuelta completa en bicicleta a • Calcula las distancias recorridas entre 0
una pista circular de 10 m de radio. min y 20 min, y entre 20 min y 40 min. ¿Son
iguales las distancias en los dos casos?
• ¿Cuánto vale el desplazamiento?
• ¿Qué distancia medida sobre la trayectoria 0 m 500 m 1000 m
ha re corrido?
6. Al empezar un paseo, Natalia recorre 20 m en 10 min 30 min
los primeros 10 s. En los siguientes 20 s, recorre 0 min 20 min
45 m más.
40 min
• Representa estos datos en un sistema de casa 1500 m
referencia tomando tiempo cero cuando
Natalia empieza el paseo. Prohibida su reproducción
50 min
• ¿Qué distancia ha recorrido en los 30 s?
escuela

27