Page 28 - Module & More Matematik Tambahan Tg5

Kertas 2
Tinggi (cm) / Height (cm)
40
3
x + 1
1. Lakarkan graf y = kos 2x + 1 dan y = kos
2
bagi 0° < x < 360° pada graf yang disediakan
20
di bawah. Kemudian, tandakan ⊗ pada titik
persilangan dua graf tersebut.
Tanah
Masa (s)
Sketch the graph of y = cos 2x + 1 and y = cos
0
Ground
Time (s)
3
0° < x < 360° on the graph provided. Hence, mark ⊗ on
(a) Nyatakan fungsi trigonometri yang mewakili
the points of intersection of the two graphs.
tinggi pedal basikal itu daripada tanah, H
Jawapan / Answer :
dengan masa, t.
State the trigonometric function that represents the

height of the bicycle pedal from the ground, H and
y 2 x + 1 for Matematik Tingkatan 5 Bab 6 Nisbah dan Graf Fungsi Trigonometri
3
y = kos x + 1 y = kos 3x + 1 time, t.
2
2 (b) Berapakah diameter putaran pedal basikal
itu?
Matematik Tambahan Tingkatan 5 Bab 1 Sukatan Membulat
1 What is the diameter of the bicycle pedal rotation?
Jawapan / Answer :
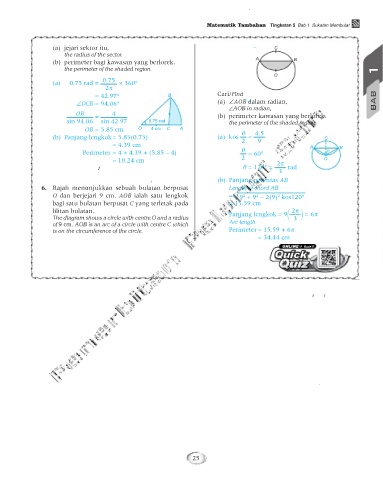
(a) jejari sektor itu, 120° 180° 240° 300° 360° x (a) a = 40 – 20 = 10 ∴ H = 10 kos 24t + 30
C
0
60°
the radius of the sector. 2 H = 10 cos 24t + 30
(b) perimeter bagi kawasan yang berlorek. b = 360° A = 24 B
the perimeter of the shaded region. 15 1
c = 10 + 20 = 30 O
2. Rajah berikut menunjukkan tinggi pedal sebuah
(a) 0.75 rad = 0.75 × 360°
2π
basikal semasa dikayuh pada laju seragam dalam (b) Diameter putaran pedal basikal

Diameter of the bicycle pedal rotation
tempoh seminit. B Cari/Find
= 42.97°
= 40 – 20 = 20 cm

The diagram shows the height of a bicycle pedal while (a) ∠AOB dalam radian, BAB
∠OCB = 94.06°
pedalling at a constant speed in a minute. ∠AOB in radian,
OB = 4 = (b) perimeter kawasan yang berlorek.
sin 94.06 sin 42.97 0.75 rad the perimeter of the shaded region.
Sudut
Sudut
O
C
OB = 5.85 cm Sudut A KBAT
4 cm
=
KBAT
KBAT
KBAT
q
(b) Panjang lengkok = 5.85(0.75) (a) kos = 4.5 C Ekstra
2
9
= 4.39 cm A B 6
q
Perimeter = 4 + 4.39 + (5.85 – 4)

Populasi satu spesis ikan di suatu tasik diwakili oleh Jawapan / Answer:
= 60°
2
O
fungsi P(t) = 4 800 sin t + 6 400, dengan P ialah (a) Populasi maksimum ikan / Maximum fish population
= 10.24 cm
2π
q = 120° =
populasi ikan, t ialah masa dalam hari dan 0 < x < 360. = 4 800 + 6 400 = 11 222 rad
3
The population of a species of fish in a lake is represented Populasi minimum ikan / Minimum fish population BAB
by function P(t) = 4 800 sin t + 6 400, where P is the fish (b) Panjang perentas AB
= 4 800 + 6 400 = 1 600
population, t is the time in days and 0 < x < 360.
6. Rajah menunjukkan sebuah bulatan berpusat Length of chord AB
(a) Hitung populasi maksimum dan minimum ikan
O dan berjejari 9 cm. AOB ialah satu lengkok (b) t = 0, 180, 360 2 2
=
2
9 + 9 − 2(9) kos120°
itu.
bagi satu bulatan berpusat C yang terletak pada = 15.59 cm

Calculate the maximum and minimum population of
lilitan bulatan. (c) 4 800 sin t + 6 400 = 1889  2π  = 6π
the fish.

Panjang lengkok = 9
The diagram shows a circle with centre O and a radius sin t = –0.9398 3
(b) Pada hari keberapakah populasi ikan mencapai 6
Arc length
–1
of 9 cm. AOB is an arc of a circle with centre C which a = sin 0.9398
400 ekor?
Perimeter = 15.59 + 6π
is on the circumference of the circle. = 70

During which days does the fish population reach 6

= 34.44 cm
400? ∴ t = 180 + 70, 360 – 70
(c) Hitung nilai-nilai t apabila terdapat 1 889 ekor = 250, 290 Kuiz 6 1
ikan.
Calculate the values of t when there was 1 889 fishes.
93 © Penerbitan Pelangi Sdn. Bhd.
25