Page 15 - Top Class F5 - Mathematics (Chapter 2)
P. 15
Mathematics Form 5 Chapter 2 Matrices
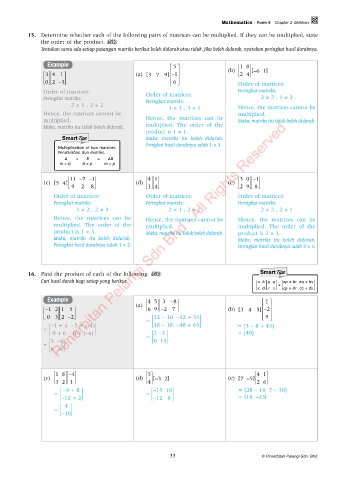
15. Determine whether each of the following pairs of matrices can be multiplied. If they can be multiplied, state
the order of the product. PL 2
Tentukan sama ada setiap pasangan matriks berikut boleh didarab atau tidak. Jika boleh didarab, nyatakan peringkat hasil darabnya.
Example 5 (b) [–6 1]
1 8
2 4
3 4 1
(a) [3 7 9] –1 Order of matrices:
0 2 –3
6
Order of matrices: Order of matrices: Peringkat matriks:
Peringkat matriks: Peringkat matriks: 2 × 2 , 1 × 2
2 × 1 , 2 × 2
1 × 3 , 3 × 1 Hence, the matrices cannot be
Hence, the matrices cannot be multiplied.
multiplied. Hence, the matrices can be Maka, matriks itu tidak boleh didarab.
Maka, matriks itu tidak boleh didarab. multiplied. The order of the
product is 1 × 1.
Maka, matriks itu boleh didarab.
Pringkat hasil darabnya ialah 1 × 1.
Multiplication of two matrices:
Pendaraban dua matriks:
A × B = AB
m × n n × p m × p
3 0 –1
4 1
(c) [5 4] 11 –7 –1 (d) (e)
1 4
2
2 9 8
9
8
Order of matrices: Order of matrices: Order of matrices:
Peringkat matriks: Peringkat matriks: Peringkat matriks:
1 × 2 , 2 × 3 2 × 1 , 2 × 1 2 × 2 , 2 × 1
Hence, the matrices can be Hence, the matrices cannot be Hence, the matrices can be
multiplied. The order of the multiplied. multiplied. The order of the
product is 1 × 3. Maka, matriks itu tidak boleh didarab. product is 2 × 1.
Maka, matriks itu boleh didarab. Maka, matriks itu boleh didarab.
Peringkat hasil darabnya ialah 1 × 3. Peringkat hasil darabnya ialah 2 × 1.
16. Find the product of each of the following. PL 3
Cari hasil darab bagi setiap yang berikut. a b p q ap + br aq + bs
cp + dr cq + ds
=
c d r s
Example 4 5 3 –8 1
(a)
–1 2 1 5 6 9 –2 7 (b) [3 4 5] –2
0 3 2 –2
= 12 – 10 –32 + 35 9
–1 + 4 –5 + (–4) 18 – 18 –48 + 63 = [3 – 8 + 45]
= 0 + 6 0 + (–6) 2 3 = [40]
=
= 3 –9 0 15
6 –6
1 8 –4
5
4 1
(c) 3 2 1 (d) 4 [–3 2] (e) [7 –5] 2 6
–4 + 8 –15 10 = [28 – 10 7 – 30]
= –12 + 2 = –12 8 = [18 –23]
4
= –10
33 © Penerbitan Pelangi Sdn. Bhd.