Page 29 - Focus SPM 2022 - Additional Mathematics

Additional Mathematics SPM Chapter 1 Functions

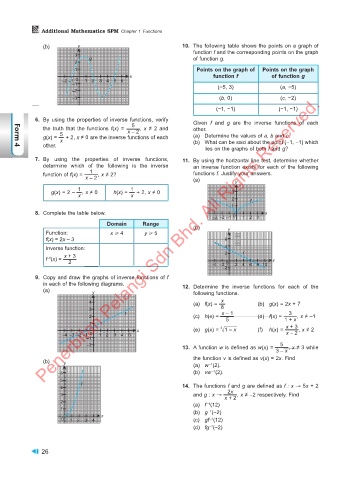
(b) y 10. The following table shows the points on a graph of
function f and the corresponding points on the graph
3 g of function g.
2
1 Points on the graph of Points on the graph
x function f of function g
–2 –1 0 1 2 3 4 5 6
–1 (−5, 3) (a, −5)
–2
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
–3 (b, 0) (c, −2)
(−1, −1) (−1, −1)
6. By using the properties of inverse functions, verify Given f and g are the inverse functions of each
5
the truth that the functions f(x) = x – 2 , x ≠ 2 and other.
g(x) = 5 x + 2, x ≠ 0 are the inverse functions of each (a) Determine the values of a, b and c.
other. (b) What can be said about the point (−1, −1) which
lies on the graphs of both f and g?
Form 4
7. By using the properties of inverse functions, 11. By using the horizontal line test, determine whether
determine which of the following is the inverse an inverse function exists for each of the following
1
function of f(x) = , x ≠ 2? functions f. Justify your answers.
x – 2 (a) y
1 1
g(x) = 2 – , x ≠ 0 h(x) = + 2, x ≠ 0 3
x x
2 f
1
8. Complete the table below. x
–3 –2 –1 0 1 2 3
Domain Range
(b) y
Function: x > 4 y > 5
f(x) = 2x – 3 6
Inverse function: 4
x + 3 2 f
f (x) =
–1
2 –4 –2 0 2 4 6 8 10 x
–2
9. Copy and draw the graphs of inverse functions of f
in each of the following diagrams. 12. Determine the inverse functions for each of the
(a) y following functions.
4 (a) f(x) = x (b) g(x) = 2x + 7
3 8 x – 1 3
2 f (c) h(x) = 5 (d) f(x) = 1 + x , x ≠ –1
1 x + 3
3
1 – x
x (e) g(x) = ABBBB (f) h(x) = x – 2 , x ≠ 2
–4 –3 –2 –1 0 1 2 3 4 5
–1
–2 5
13. A function w is defined as w(x) = , x ≠ 3 while
3 – x
the function v is defined as v(x) = 2x. Find
(b) y (a) w (2).
–1
–1

6 (b) vw (2).
5
4 f 14. The functions f and g are defined as f : x → 5x + 2
2x
3 and g : x → x + 2 , x ≠ –2 respectively. Find
2 (a) f (12)
–1
1 (b) g (−2)
–1
x
0 1 2 3 4 (c) gf (12)
–1
(d) fg (–2)
–1
26