Page 11 - Ranger SPM 2022 - Additional Mathematics

Additional Mathematics SPM Chapter 2 Quadratic Functions
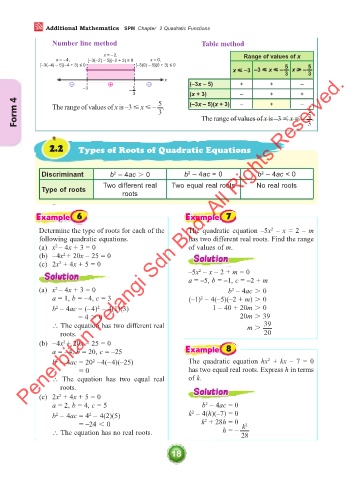
Number line method Table method

x = –2, Range of values of x
x = –4, [–3(–2) – 5](–2 + 3) ≥ 0 x = 0,
[–3(–4) – 5](–4 + 3) ≤ 0 [–3(0) – 5](0 + 3) ≤ 0 5 5
x  –3 –3  x  – 3 x  – 3
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
x
– + – (–3x – 5) + + –
–3 – 5
3 5 (x + 3) – + +
Form 4 The range of values of x is –3  x  – . (–3x – 5)(x + 3) – + – 5
3
The range of values of x is –3  x  – .
3

2.2 Types of Roots of Quadratic Equations

2
2
Discriminant b – 4ac  0 b – 4ac = 0 b – 4ac < 0
2
Two different real Two equal real roots No real roots
Type of roots
roots
Example 6 Example 7
Determine the type of roots for each of the The quadratic equation –5x – x = 2 – m
2
following quadratic equations. has two different real roots. Find the range
(a) x – 4x + 3 = 0 of values of m.
2
(b) –4x + 20x – 25 = 0
2
(c) 2x + 4x + 5 = 0 Solution
2
–5x – x – 2 + m = 0
2
Solution a = –5, b = –1, c = –2 + m
(a) x – 4x + 3 = 0 b – 4ac  0
2
2
a = 1, b = –4, c = 3 (–1) – 4(–5)(–2 + m)  0
2
b – 4ac = (–4) – 4(1)(3) 1 – 40 + 20m  0
2
2
= 4  0 20m  39
∴ The equation has two different real m  39
roots. 20
2
(b) –4x + 20x – 25 = 0
a = –4, b = 20, c = –25 Example 8
2
b – 4ac = 20 –4(–4)(–25) The quadratic equation hx + kx – 7 = 0
2
2
= 0 has two equal real roots. Express h in terms
∴ The equation has two equal real of k.
roots.
(c) 2x + 4x + 5 = 0 Solution
2
a = 2, b = 4, c = 5 b – 4ac = 0
2
2
b – 4ac = 4 – 4(2)(5) k – 4(h)(–7) = 0
2
2
2
= –24  0 k + 28h = 0 k 2
∴ The equation has no real roots. h = – 28
18
02 Ranger Add Mathematics Tg4.indd 18 25/02/2022 9:10 AM