Page 15 - Ranger SPM 2022 - Additional Mathematics

Additional Mathematics SPM Chapter 2 Quadratic Functions

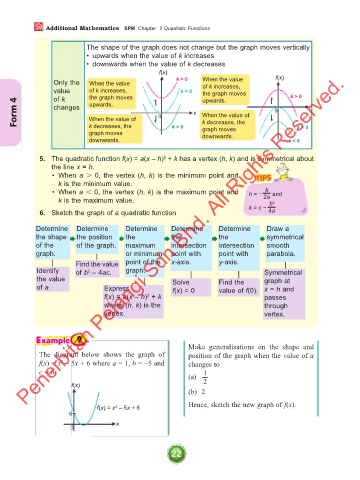
The shape of the graph does not change but the graph moves vertically
• upwards when the value of k increases
• downwards when the value of k decreases
f(x)
Penerbitan Pelangi Sdn Bhd. All Rights Reserved.
Only the When the value k > 0 When the value f(x)
of k increases,
value of k increases, k = 0 the graph moves k > 0
the graph moves
of k
upwards.
Form 4 changes upwards. 0 x When the value of 0 x
When the value of
k decreases, the
k decreases, the
graph moves k < 0 graph moves k = 0
downwards.
downwards. k < 0
5. The quadratic function f(x) = a(x – h) + k has a vertex (h, k) and is symmetrical about
2
the line x = h.
• When a  0, the vertex (h, k) is the minimum point and TIPS
k is the minimum value.
• When a  0, the vertex (h, k) is the maximum point and h = − b and
k is the maximum value. 2a b 2
k = c −
6. Sketch the graph of a quadratic function 4a

Determine Determine Determine Determine Determine Draw a
the shape the position the the the symmetrical
of the of the graph. maximum intersection intersection smooth
graph. or minimum point with point with parabola.
Find the value point of the x-axis. y-axis.
Identify of b – 4ac. graph. Symmetrical
2
the value Solve Find the graph at
of a. Express f(x) = 0 value of f(0). x = h and
f(x) = a(x – h) + k passes
2
where (h, k) is the through
vertex. vertex.

Example 9
Make generalisations on the shape and
The diagram below shows the graph of position of the graph when the value of a
f(x) = x – 5x + 6 where a = 1, b = –5 and changes to
2
c = 6. 1
(a)
f(x) 2
(b) 2

f(x) = x – 5x + 6 Hence, sketch the new graph of f(x).
2
6
x
0

22

02 Ranger Add Mathematics Tg4.indd 22 25/02/2022 9:10 AM