Page 437 - MARSIUM'21 COMP OF PAPER

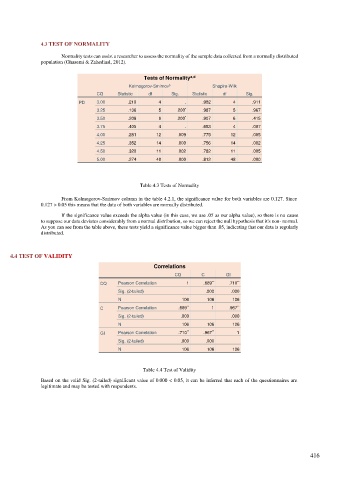
4.3 TEST OF NORMALITY

Normality tests can assist a researcher to assess the normality of the sample data collected from a normally distributed
population (Ghasemi & Zahediasl, 2012).

Tests of Normality a,d

Kolmogorov-Smirnov b Shapiro-Wilk
CQ Statistic df Sig. Statistic df Sig.
PD 3.00 .210 4 . .982 4 .911
3.25 .136 5 .200 * .987 5 .967
3.50 .209 6 .200 * .907 6 .415
3.75 .405 4 . .683 4 .007
4.00 .281 12 .009 .775 12 .005
4.25 .352 14 .000 .756 14 .002
4.50 .320 11 .002 .782 11 .005
5.00 .274 48 .000 .812 48 .000

Table 4.3 Tests of Normality

From Kolmogorov-Smirnov column in the table 4.2.1, the significance value for both variables are 0.127. Since
0.127 > 0.05 this means that the data of both variables are normally distributed.
If the significance value exceeds the alpha value (in this case, we use .05 as our alpha value), so there is no cause
to suppose our data deviates considerably from a normal distribution, so we can reject the null hypothesis that it's non- normal.
As you can see from the table above, these tests yield a significance value bigger than .05, indicating that our data is regularly
distributed.

4.4 TEST OF VALIDITY

Correlations
CQ C GI
**
**
CQ Pearson Correlation 1 .689 .710
Sig. (2-tailed) .000 .000
N 106 106 106
**
**
C Pearson Correlation .689 1 .967
Sig. (2-tailed) .000 .000
N 106 106 106
**
**
GI Pearson Correlation .710 .967 1

Sig. (2-tailed) .000 .000
N 106 106 106

Table 4.4 Test of Validity

Based on the valid Sig. (2-tailed) significant value of 0.000 < 0.05, it can be inferred that each of the questionnaires are
legitimate and may be tested with respondents.

416