Page 750 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

726 MÉTODOS DE RUNGE-KUTTA

Esta última conclusión tiene un sentido intuitivo, puesto que el método de Euler usa
segmentos de línea recta para aproximar la solución. De ahí que al método de Euler se
le conozca como un método de primer orden.
También deberá observarse que este patrón general rige a los métodos de orden supe-
rior de un paso, que se describen en las siguientes páginas. Es decir, un método de n-ési-
mo orden dará resultados perfectos si la solución de la EDO es un polinomio de n-ésimo
n
grado. Además, el error de truncamiento local será O(h n+1 ); y el error global, O(h ).
EJEMPLO 25.3 Efecto de un tamaño de paso reducido en el método de Euler
Planteamiento del problema. Repita el cálculo del ejemplo 25.1, pero ahora use un
tamaño de paso igual a 0.25.
Solución. Los cálculos se repiten, y los resultados se recopilan en la figura 25.4a). Al
reducir el tamaño de paso a la mitad, el valor absoluto del error global promedio dismi-

y
h = 0.5
h = 0.25

4

Solución verdadera

0
0 2 4 x
a)
y

0
2 4 x
Estimada

Verdadera
– 0.5

b)

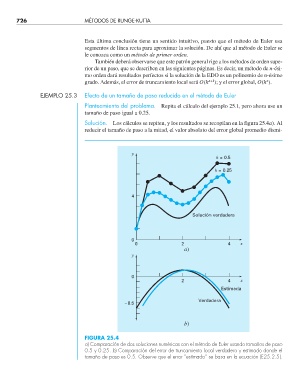
FIGURA 25.4
a) Comparación de dos soluciones numéricas con el método de Euler usando tamaños de paso
0.5 y 0.25. b) Comparación del error de truncamiento local verdadero y estimado donde el
tamaño de paso es 0.5. Observe que el error “estimado” se basa en la ecuación (E25.2.5).

6/12/06 14:01:57
Chapra-25.indd 726 6/12/06 14:01:57
Chapra-25.indd 726