Page 755 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

25.1 MÉTODO DE EULER 731

y
60
Lineal

40
No lineal

20

0
0 5 10 15 t

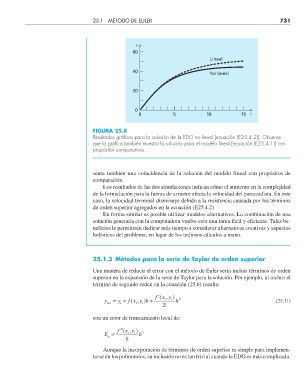
FIGURA 25.8
Resultados gráfi cos para la solución de la EDO no lineal [ecuación (E25.4.2)]. Observe
que la gráfi ca también muestra la solución para el modelo lineal [ecuación (E25.4.1)] con
propósitos comparativos.

senta también una coincidencia de la solución del modelo lineal con propósitos de
comparación.
Los resultados de las dos simulaciones indican cómo el aumento en la complejidad
de la formulación para la fuerza de arrastre afecta la velocidad del paracaidista. En este
caso, la velocidad terminal disminuye debido a la resistencia causada por los términos
de orden superior agregados en la ecuación (E25.4.2).
En forma similar es posible utilizar modelos alternativos. La combinación de una
solución generada con la computadora vuelve esto una tarea fácil y eficiente. Tales be-
neficios le permitirán dedicar más tiempo a considerar alternativas creativas y aspectos
holísticos del problema, en lugar de los tediosos cálculos a mano.

25.1.3 Métodos para la serie de Taylor de orden superior
Una manera de reducir el error con el método de Euler sería incluir términos de orden
superior en la expansión de la serie de Taylor para la solución. Por ejemplo, al incluir el
término de segundo orden en la ecuación (25.6) resulta:
′(,
f x y h +
i
i
y i+1 = y + (, ) fx y ) h 2 (25.11)
i
i
i
2!
con un error de truncamiento local de:
x y
E = f ′′(, ) h 3
i
i
a
6
Aunque la incorporación de términos de orden superior es simple para implemen-
tarse en los polinomios, su inclusión no es tan trivial cuando la EDO es más complicada.

6/12/06 14:01:58
Chapra-25.indd 731 6/12/06 14:01:58
Chapra-25.indd 731