Page 43 - Euclid's Elements of Geometry
P. 43
ST EW aþ.
πληρώματί ἐστιν ἴσον. the remaining complement KD. ELEMENTS BOOK 1
Α Θ ∆ A H D
Κ K
Ε Ζ E F
mdþ
Β Η Γ B G C
Παντὸς ἄρα παραλληλογράμμου χωρίου τῶν περὶ τὴν Thus, for any parallelogramic figure, the comple-
διάμετρον παραλληλογράμμων τὰ παραπληρώματα ἴσα ἀλλή- ments of the parallelograms about the diagonal are equal
λοις ἐστίν· ὅπερ ἔδει δεῖξαι. to one another. (Which is) the very thing it was required
to show.
Proposition 44
.
Παρὰ τὴν δοθεῖσαν εὐθεῖαν τῷ δοθέντι τριγώνῳ ἴσον πα- To apply a parallelogram equal to a given triangle to
ραλληλόγραμμον παραβαλεῖν ἐν τῇ δοθείσῃ γωνίᾳ εὐθυγράμ- a given straight-line in a given rectilinear angle.
μῳ.
∆ D
Γ C
Ζ Ε Κ F E K
Η Μ G M
Β B
Θ Α Λ H A L
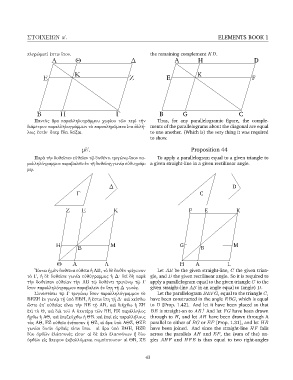
῎Εστω ἡ μὲν δοθεῖσα εὐθεῖα ἡ ΑΒ, τὸ δὲ δοθὲν τρίγωνον Let AB be the given straight-line, C the given trian-
τὸ Γ, ἡ δὲ δοθεῖσα γωνία εὐθύγραμμος ἡ Δ· δεῖ δὴ παρὰ gle, and D the given rectilinear angle. So it is required to
τὴν δοθεῖσαν εὐθεῖαν τὴν ΑΒ τῷ δοθέντι τριγώνῳ τῷ Γ apply a parallelogram equal to the given triangle C to the
ἴσον παραλληλόγραμμον παραβαλεῖν ἐν ἴσῃ τῇ Δ γωνίᾳ. given straight-line AB in an angle equal to (angle) D.
Συνεστάτω τῷ Γ τριγώνῳ ἴσον παραλληλόγραμμον τὸ Let the parallelogram BEFG, equal to the triangle C,
ΒΕΖΗ ἐν γωνίᾳ τῇ ὑπὸ ΕΒΗ, ἥ ἐστιν ἴση τῇ Δ· καὶ κείσθω have been constructed in the angle EBG, which is equal
ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΒΕ τῇ ΑΒ, καὶ διήχθω ἡ ΖΗ to D [Prop. 1.42]. And let it have been placed so that
†
ἐπὶ τὸ Θ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΒΗ, ΕΖ παράλληλος BE is straight-on to AB. And let FG have been drawn
ἤχθω ἡ ΑΘ, καὶ ἐπεζεύχθω ἡ ΘΒ. καὶ ἐπεὶ εἰς παραλλήλους through to H, and let AH have been drawn through A
τὰς ΑΘ, ΕΖ εὐθεῖα ἐνέπεσεν ἡ ΘΖ, αἱ ἄρα ὑπὸ ΑΘΖ, ΘΖΕ parallel to either of BG or EF [Prop. 1.31], and let HB
γωνίαι δυσὶν ὀρθαῖς εἰσιν ἴσαι. αἱ ἄρα ὑπὸ ΒΘΗ, ΗΖΕ have been joined. And since the straight-line HF falls
δύο ὀρθῶν ἐλάσσονές εἰσιν· αἱ δὲ ἀπὸ ἐλασσόνων ἢ δύο across the parallels AH and EF, the (sum of the) an-
ὀρθῶν εἰς ἄπειρον ἐκβαλλόμεναι συμπίπτουσιν· αἱ ΘΒ, ΖΕ gles AHF and HFE is thus equal to two right-angles
43