Page 79 - ArithBook5thEd ~ BCC

3.4 Multiplication of Fractions

Fractions are numbers in their own right, and we will recall how to add, subtract, multiply and divide
them. We begin with multiplication, since it is one of the easiest operations to perform.
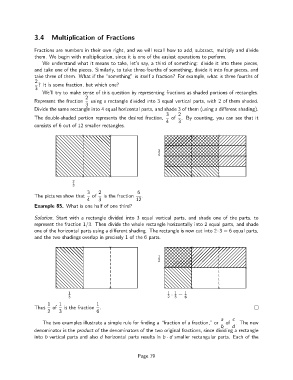
We understand what it means to take, let’s say, a third of something: divide it into three pieces,
and take one of the pieces. Similarly, to take three-fourths of something, divide it into four pieces, and
take three of them. What if the “something” is itself a fraction? For example, what is three fourths of
2
? It is some fraction, but which one?
3
We’ll try to make sense of this question by representing fractions as shaded portions of rectangles.
2
Represent the fraction using a rectangle divided into 3 equal vertical parts, with 2 of them shaded.
3
Divide the same rectangle into 4 equal horizontal parts, and shade 3 of them (using a different shading).
3 2
The double-shaded portion represents the desired fraction, of .By counting, you can see that it
4 3
consists of 6 out of 12 smaller rectangles.

× × × ×

3
4 × ×

× × × ×
2
3
3 2 6
The pictures show that of is the fraction .
4 3 12
Example 85. What is one half of one third?

Solution. Start with a rectangle divided into 3 equal vertical parts, and shade one of the parts, to
represent the fraction 1/3. Then divide the whole rectangle horizontally into 2 equal parts, and shade
one of the horizontal parts using a different shading. The rectangleis now cut into 2·3 = 6 equal parts,
and the two shadings overlap in precisely 1 of the 6 parts.

× × × ×
1
2
× ×

× × × ×
1 1 1 = 1
3 2 · 3 6
1 1 1
Thus of is the fraction .
2 3 6
a c
The two examples illustrate a simple rule for finding a “fraction of a fraction,” or of .The new
b d
denominator is the product of the denominators of the two original fractions, since dividing a rectangle
into b vertical parts and also d horizontal parts results in b · d smaller rectangular parts. Each of the

Page 79