Page 33 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
5 Additional Mathematics Chapter 3 Integration

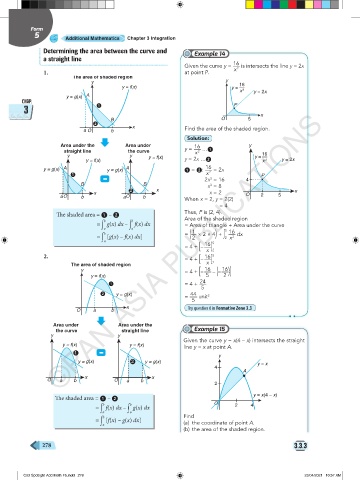
Determining the area between the curve and Example 14
a straight line
Given the curve y = 16 is intersects the line y = 2x
2
1. at point P. x
The area of shaded region
y y 16
y = f(x) y = ––
x 2 y = 2x
y = g(x) A
CHAP. P
3
x
B O 5

x Find the area of the shaded region.
a O b
Solution:
Area under the Area under 16 y
straight line the curve y = x 2 …1
y y y = f(x) y = 16
––
y = f(x) y = 2x …2 x 2 y = 2x
y = g(x) A y = g(x) A 1 = 2: 16 2 = 2x
1 x P
– 2x = 16 4
3
B B x = 8
3
2 x x
x x = 2 O
a O b a O b When x = 2, y = 2(2) 2 5
= 4
Thus, P is (2, 4).
The shaded area = 1 – 2 Area of the shaded region
∫
∫
b
b
= g(x) dx – f(x) dx = Area of triangle + Area under the curve
a
a
5
∫
b
= [g(x) – f(x) dx] = ( 1 × 2 × 4 + 16 2 dx
) ∫ 2 x
2
a
[ ]
= 4 + – 16 5 2
x
[ ]
2. ©PAN ASIA PUBLICATIONS
16
5
= 4 + –
The area of shaded region x 2
( )]
[
y = 4 + – 16 – – 16
y = f(x) 5 2
24
= 4 +
5
y = g(x) = 44 unit 2
5
x Try question 6 in Formative Zone 3.3
O a b
Area under Area under the
the curve straight line Example 15
y y
Given the curve y = x(4 – x) intersects the straight
y = f(x) y = f(x) line y = x at point A.
1 –
y
y = g(x) 2 y = g(x) y = x
4
A
x x
O a b O a b
2
The shaded area = 1 – 2 y = x(4 – x)
∫
∫
b
b
= f(x) dx – g(x) dx O 2 4
a a
∫
b
= [f(x) – g(x) dx] Find
a (a) the coordinate of point A.
(b) the area of the shaded region.
278 3.3.3
C03 Spotlight Add Math F5.indd 278 23/04/2021 10:57 AM