Page 37 - Spotlight A+ SPM Additional Mathematics Form 4 & 5

Form
5 Additional Mathematics Chapter 5 Probability Distribution

5. If Z is a standard normal distribution with mean 8. If the probability is between z-score, which is a
is 0 and standard deviation is 1, thus the value and b:
of z gives the probability of standard normal f(z)
distribution.
f(z)

z
O a b
z
O a
P(a , Z , b) = P(Z . a) – P(Z . b)
©PAN ASIA PUBLICATIONS

Probability by using Standard Example 23
Normal Distribution Table
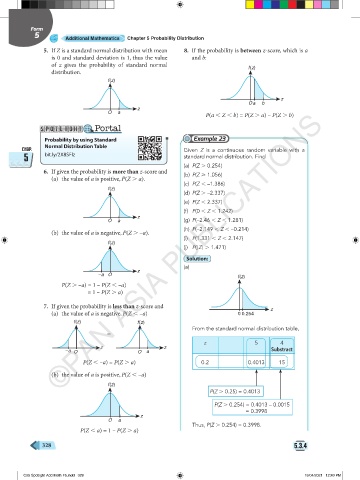
CHAP. Given Z is a continuous random variable with a
5 bit.ly/2X8SFlz standard normal distribution. Find
(a) P(Z . 0.254)
6. If given the probability is more than z-score and (b) P(Z > 1.056)
(a) the value of a is positive, P(Z . a).
(c) P(Z , –1.386)
f(z)
(d) P(Z . –2.337)
(e) P(Z , 2.337)
(f) P(0 , Z , 1.242)
z
O a (g) P(–2.46 , Z , 1.281)
(b) the value of a is negative, P(Z . –a). (h) P(–2.149 , Z , –0.214)
(i) P(1.331 , Z , 2.147)
f(z)
(j) P(| Z | . 1.471)
Solution:
(a)
z
–a O
f(z)
P(Z . –a) = 1 – P(Z , –a)
= 1 – P(Z . a)

7. If given the probability is less than z-score and z
(a) the value of a is negative, P(Z , –a) 0 0.254
f(z) f(z)
From the standard normal distribution table,
=
z 5 4
z z
–a O O a Substract

P(Z , –a) = P(Z . a) 0.2 0.4013 15
(b) the value of a is positive, P(Z , –a)
f(z)
P(Z . 0.25) = 0.4013

P(Z . 0.254) = 0.4013 – 0.0015
= 0.3998
z
O a
Thus, P(Z . 0.254) = 0.3998.
P(Z , a) = 1 – P(Z . a)

328 5.3.4

C05 Spotlight Add Math F5.indd 328 19/04/2021 12:43 PM