Page 238 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

3.5 In this section we shall use vectors to derive equations of lines and planes in
3-space. We shall then use these equations to solve some basic geometric
LINES AND PLANES IN problems.
3-SPACE

Planes in 3-Space

In analytic geometry a line in 2-space can be specified by giving its slope and one of its points. Similarly, one can specify a
plane in 3-space by giving its inclination and specifying one of its points. A convenient method for describing the inclination of
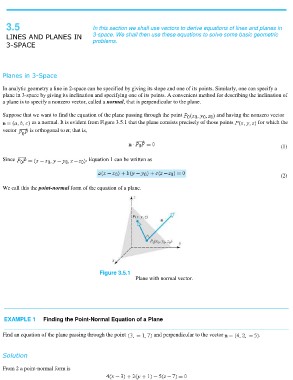
a plane is to specify a nonzero vector, called a normal, that is perpendicular to the plane.

Suppose that we want to find the equation of the plane passing through the point and having the nonzero vector

as a normal. It is evident from Figure 3.5.1 that the plane consists precisely of those points for which the

vector is orthogonal to n; that is,

(1)

Since , Equation 1 can be written as

(2)

We call this the point-normal form of the equation of a plane.

Figure 3.5.1
Plane with normal vector.

EXAMPLE 1 Finding the Point-Normal Equation of a Plane

Find an equation of the plane passing through the point and perpendicular to the vector .

Solution

From 2 a point-normal form is