Page 240 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

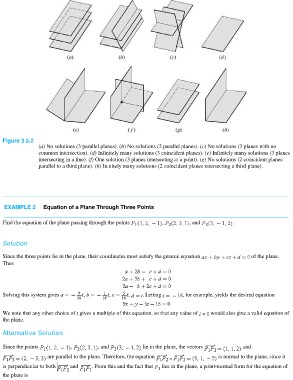
Figure 3.5.2

(a) No solutions (3 parallel planes). (b) No solutions (2 parallel planes). (c) No solutions (3 planes with no
common intersection). (d) Infinitely many solutions (3 coincident planes). (e) Infinitely many solutions (3 planes
intersecting in a line). (f) One solution (3 planes intersecting at a point). (g) No solutions (2 coincident planes
parallel to a third plane). (h) In.nitely many solutions (2 coincident planes intersecting a third plane).

EXAMPLE 2 Equation of a Plane Through Three Points

Find the equation of the plane passing through the points , , and .
of the plane.
Solution

Since the three points lie in the plane, their coordinates must satisfy the general equation
Thus

Solving this system gives , , , . Letting , for example, yields the desired equation

We note that any other choice of t gives a multiple of this equation, so that any value of would also give a valid equation of
the plane.

Alternative Solution

Since the points , , and lie in the plane, the vectors and

are parallel to the plane. Therefore, the equation is normal to the plane, since it

is perpendicular to both and . From this and the fact that lies in the plane, a point-normal form for the equation of
the plane is