Page 383 - Elementary_Linear_Algebra_with_Applications_Anton__9_edition

5.4 We usually think of a line as being one-dimensional, a plane as
two-dimensional, and the space around us as three-dimensional. It is the
BASIS AND DIMENSION primary purpose of this section to make this intuitive notion of “dimension” more
precise.

Nonrectangular Coordinate Systems

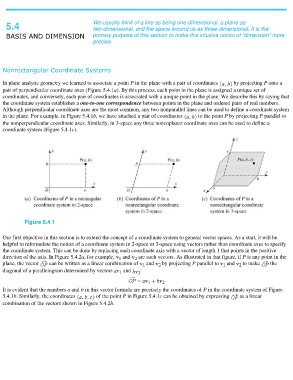
In plane analytic geometry we learned to associate a point P in the plane with a pair of coordinates by projecting P onto a

pair of perpendicular coordinate axes (Figure 5.4.1a). By this process, each point in the plane is assigned a unique set of

coordinates, and conversely, each pair of coordinates is associated with a unique point in the plane. We describe this by saying that

the coordinate system establishes a one-to-one correspondence between points in the plane and ordered pairs of real numbers.

Although perpendicular coordinate axes are the most common, any two nonparallel lines can be used to define a coordinate system

in the plane. For example, in Figure 5.4.1b, we have attached a pair of coordinates to the point P by projecting P parallel to

the nonperpendicular coordinate axes. Similarly, in 3-space any three noncoplanar coordinate axes can be used to define a

coordinate system (Figure 5.4.1c).

Figure 5.4.1

Our first objective in this section is to extend the concept of a coordinate system to general vector spaces. As a start, it will be
helpful to reformulate the notion of a coordinate system in 2-space or 3-space using vectors rather than coordinate axes to specify
the coordinate system. This can be done by replacing each coordinate axis with a vector of length 1 that points in the positive
direction of the axis. In Figure 5.4.2a, for example, and are such vectors. As illustrated in that figure, if P is any point in the
plane, the vector can be written as a linear combination of and by projecting P parallel to and to make the
diagonal of a parallelogram determined by vectors and :

It is evident that the numbers a and b in this vector formula are precisely the coordinates of P in the coordinate system of Figure

5.4.1b. Similarly, the coordinates of the point P in Figure 5.4.1c can be obtained by expressing as a linear

combination of the vectors shown in Figure 5.4.2b.