Page 135 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics

The product of vectors a and b is given as:
a × b = a i + a j × b i + b j

2
1
1
2
= a i × b i + a i × b j + a j × b i + a j × b j - - - - (1.31)
1
1
2
2
2
2
1
1
It can be observed from the example of spanner and nut, that, no torque is produced if force and
the position vector (length of spanner) are along the same axis. Hence, vector products of identical
unit vectors are zero. Therefore, the first and last terms of equation (1.31) go to zero. Also, we

know that, j × i = −k and i × j = k . Using these facts, we get:

= a i × b j + a j × b i = a b k − a b k = a b − a b k - - - - (1.32)
1 2
2
2
1
2 1
2 1
1 2
1
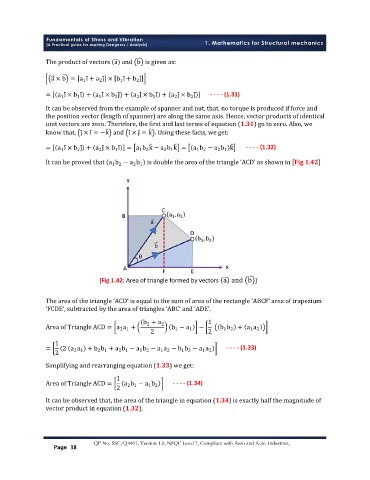
It can be proved that a b − a b is double the area of the triangle ‘ACD’ as shown in [Fig 1.42]
1 2
2 1

[Fig 1.42: Area of triangle formed by vectors a and b ]

The area of the triangle ‘ACD’ is equal to the sum of area of the rectangle ‘ABCF’ area of trapezium
‘FCDE’, subtracted by the area of triangles ‘ABC’ and ‘ADE’.

(b + a 2 1
2
Area of Triangle ACD = a a + b − a − b b + a a
1 2
1 2
1
1
2 1
2 2
1
= 2 a a + b b + a b − a b − a a − b b − a a - - - - (1.33)
1 2
1 2
1 2
2 1
2 1
2 1
1 2
2
Simplifying and rearranging equation (1.33) we get:
1
Area of Triangle ACD = a b − a b - - - - (1.34)
1 2
2 1
2
It can be observed that, the area of the triangle in equation (1.34) is exactly half the magnitude of
vector product in equation (1.32).

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 38