Page 740 - Fisika Dasar 1 - Mikrajuddin Abdullah

Bab 10 Fluida

h 1 h 2 h 3

  
A B C

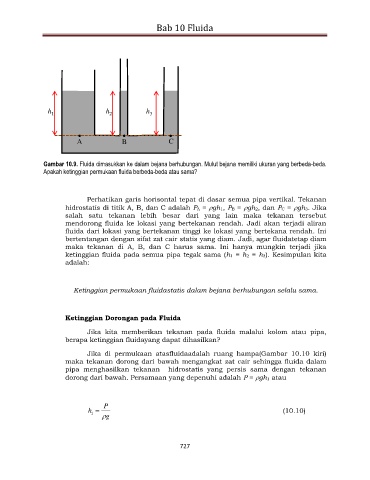
Gambar 10.9. Fluida dimasukkan ke dalam bejana berhubungan. Mulut bejana memiliki ukuran yang berbeda-beda.
Apakah ketinggian permukaan fluida berbeda-beda atau sama?

Perhatikan garis horisontal tepat di dasar semua pipa vertikal. Tekanan
hidrostatis di titik A, B, dan C adalah PA = gh1, PB = gh2, dan PC = gh3. Jika
salah satu tekanan lebih besar dari yang lain maka tekanan tersebut
mendorong fluida ke lokasi yang bertekanan rendah. Jadi akan terjadi aliran
fluida dari lokasi yang bertekanan tinggi ke lokasi yang bertekana rendah. Ini
bertentangan dengan sifat zat cair statis yang diam. Jadi, agar fluidatetap diam
maka tekanan di A, B, dan C harus sama. Ini hanya mungkin terjadi jika
ketinggian fluida pada semua pipa tegak sama (h1 = h2 = h3). Kesimpulan kita
adalah:

Ketinggian permukaan fluidastatis dalam bejana berhubungan selalu sama.

Ketinggian Dorongan pada Fluida

Jika kita memberikan tekanan pada fluida malalui kolom atau pipa,
berapa ketinggian fluidayang dapat dihasilkan?

Jika di permukaan atasfluidaadalah ruang hampa(Gambar 10.10 kiri)
maka tekanan dorong dari bawah mengangkat zat cair sehingga fluida dalam
pipa menghasilkan tekanan hidrostatis yang persis sama dengan tekanan
dorong dari bawah. Persamaan yang depenuhi adalah P = gh1 atau

P
h  g  (10.10)
1

727